题目内容
已知平面向量
=(
,-1),
=(
,
),
(1)证明:
⊥
;
(2)若存在不同时为零的实数k和g,使
=
+(g2-3)
,
=-k
+g
,且
⊥
,试求函数关系式k=f(g);
(3)椐(2)的结论,讨论关于g的方程f(g)-k=0的解的情况.
| a |
| 3 |
| b |
| 1 |
| 2 |
| ||
| 2 |
(1)证明:
| a |
| b |
(2)若存在不同时为零的实数k和g,使
| x |
| a |
| b |
| y |
| a |
| b |
| x |
| y |
(3)椐(2)的结论,讨论关于g的方程f(g)-k=0的解的情况.
(1)∵
•
=
×
+(-1)×
=0,∴
⊥
.
(2)∵
⊥
,∴
•
=0,即(
+(g2-3)
)•(-k
+g
)=0.
整理得:-k
2+[g-k(g2-3)]
•
+g(g2-3)•
2=0.
∵
•
=0,
2=4,
2=1,∴上式化为-4k+g(g2-3)=0⇒k=
g(g2-3)
(3)讨论方程
g(g2-3)=k的解的情况,可以看作曲线f(g)=
g(g2-3)与直线y=k的交
点个数.f′(g)=
g2-
,令f'(g)═0,解得g1=1,g2=-1,当g变化时,f'(g)、f(g)
的变化情况如下表:

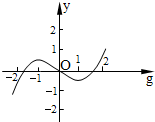
当g=-1时,f(g)有极大值
,当g=1时,f(g)有极小值-
,
而f(g)=
g(g2-3)=0时,得:g=-
,0,
,
可得:f(g)的大致图象(如右图).
于是当k>
或k<-
时,直线与曲线有且仅有一个交点,则方程有一
当k=
或k=-
时,直线与曲线有两个交点,则方程有两解;
当k=0时,直线与曲线有三个交点,但k、g不同时为零,故此时也有二解;
当?-
<k<0或0<k<
时,直线与曲线有三个交点,则方程有三个解.
| a |
| b |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| a |
| b |
(2)∵
| x |
| y |
| x |
| y |
| a |
| b |
| a |
| b |
整理得:-k
| a |
| a |
| b |
| b |
∵
| a |
| b |
| a |
| b |
| 1 |
| 4 |
(3)讨论方程
| 1 |
| 4 |
| 1 |
| 4 |
点个数.f′(g)=
| 3 |
| 4 |
| 3 |
| 4 |
的变化情况如下表:

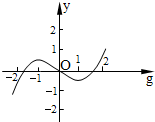
当g=-1时,f(g)有极大值
| 1 |
| 2 |
| 1 |
| 2 |
而f(g)=
| 1 |
| 4 |
| 3 |
| 3 |
可得:f(g)的大致图象(如右图).
于是当k>
| 1 |
| 2 |
| 1 |
| 2 |
当k=
| 1 |
| 2 |
| 1 |
| 2 |
当k=0时,直线与曲线有三个交点,但k、g不同时为零,故此时也有二解;
当?-
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
