题目内容
13.已知函数f(x)=|x+1|+|2x-2|.(1)解不等式f(x)>5;
(2)若关于x的方程$\frac{1}{f(x)}$-5=t的解集为空集,求实数t的取值范围.
分析 (1)化简函数的解析式为函数f(x)=|x+1|+|2x-2|=$\left\{\begin{array}{l}{-3x+1,x<-1}\\{-x+3,-1≤x≤1}\\{3x-1,x>1}\end{array}\right.$分类讨论求得原不等式解集.
(2)由(1)中分段函数f(x)的解析式可得f(x)的单调性,由此求得函数f(x)的值域,可得$\frac{1}{f(x)}$的取值范围,再根关于x的方程$\frac{1}{f(x)}$-5=t的解集为空集,求得实数t的取值范围.
解答 解:(1)函数f(x)=|x+1|+|2x-2|=$\left\{\begin{array}{l}{-3x+1,x<-1}\\{-x+3,-1≤x≤1}\\{3x-1,x>1}\end{array}\right.$
当x>1时,由3x-1>5解得:x>2;当-1≤x≤1时,由-x+3>5得x<-22 (舍去).
当x<-1时,由-3x+1>5,解得x<-$\frac{4}{3}$.
所以原不等式解集为{x|x<-$\frac{4}{3}$或x>2}.
(2)由(1)中分段函数f(x)的解析式可知:f(x)在区间(-∞,1)上单调递减,在区间(1,+∞)上单调递增.
并且f(x)的最小值为f(1)=2,所以函数f(x)的值域为[2,+∞),
从而$\frac{1}{f(x)}$的取值范围是(0,$\frac{1}{2}$],
根据关于x的方程$\frac{1}{f(x)}$-5=t的解集为空集,可得t+5≤0或t+5>$\frac{1}{2}$
所以实数t的取值范围是(-∞,-5]或(-$\frac{9}{2}$,+∞).
点评 本题主要考查带有绝对值的函数,绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.

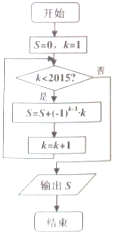 阅读如图所示的框图,运行相应的程序,则输出S的值为( )
阅读如图所示的框图,运行相应的程序,则输出S的值为( )| A. | -1008 | B. | -1007 | C. | 1007 | D. | 1008 |
| A. | c<b<a | B. | b<c<a | C. | a<b<c | D. | a<c<b |
 在三棱柱ABC-A1B1C1中,侧棱AA1⊥平面AB1C1,AA1=1,底面△ABC是边长为2的正三角形,则此三棱柱的体积为$\sqrt{2}$.
在三棱柱ABC-A1B1C1中,侧棱AA1⊥平面AB1C1,AA1=1,底面△ABC是边长为2的正三角形,则此三棱柱的体积为$\sqrt{2}$.