题目内容
2．已知函数f（x）=2x+x，g（x）=log2x+x，h（x）=lnx+x，若f（a）=g（b）=h（c）=0，则（ ）| A． | c＜b＜a | B． | b＜c＜a | C． | a＜b＜c | D． | a＜c＜b |
分析 f（a）=g（b）=h（c）=0即为函数y=2x，y=log2x，y=lnx与y=-x的交点的横坐标分别为a，b，c，画出它们的图象，即可得到a，b，c的大小．
解答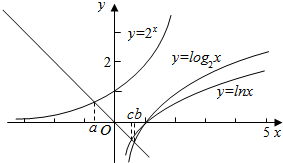 
解：f（a）=g（b）=h（c）=0
即为函数y=2x，y=log2x，y=lnx
与y=-x的交点的横坐标分别为a，b，c，
画出它们的图象，由图象可得，
a＜c＜b．
故选：D．
点评 本题考查函数的零点的判断和比较，运用函数和方程的思想和数形结合的思想方法是解题的关键．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
13．设函数f（x）=（2x+a）n，其中n=6${∫}_{0}^{\frac{π}{2}}$cosxdx，$\frac{f′（0）}{f（0）}$=-12，则f（x）的展开式中x4的系数是（ ）
| A． | -240 | B． | 240 | C． | -60 | D． | 60 |
17．设集合M={x|x2-4x+3≤0}，N={x|log2x≤1}，则M∪N=（ ）
| A． | [1，2] | B． | [1，2） | C． | [0，3] | D． | （0，3] |
14．
函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的图象如图，为了得到g（x）=Asinωx的图象，则只需将f（x）的图象（ ）
函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的图象如图，为了得到g（x）=Asinωx的图象，则只需将f（x）的图象（ ）| A． | 向右平移$\frac{π}{6}$ | B． | 向右平移$\frac{π}{12}$ | C． | 向左平移$\frac{π}{6}$ | D． | 向左平移$\frac{π}{12}$ |
如图，函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|≤$\frac{π}{2}$）的图象与坐标轴的三个交点为P，Q，R，且P（1，0），Q（m，0）（m＞0），∠PQR=$\frac{π}{4}$，M为QR的中点，|PM|=$\sqrt{5}$．