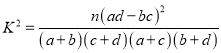Question

【题目】A.如图所示, 是园内两条弦和的交点,过延长线上一点作圆的切线, 为切点,已知求证:

B.已知矩阵 , .求矩阵,使得

C.在平面直角坐标系中,直线的参数方程为 (为参数),以坐标原点为极点, 轴正半轴为极轴的极坐标系中,曲线的极坐标方程为,已知直线与曲线相交于两点,求线段的长.

D.已知都是正数,且,求证:

Answer 1

【答案】A:详见解析；B： ；

C: ；D:详见解析.

【解析】试题分析：A．由切割线定理及三角形相似可以 ，所以 ．

B． 由矩阵变化公式可得． C．根据参数方程及极坐标方程与普通方程转化公式处理．D．由均值不等式可以得证．

试题解析：A．由切割线定理得 ，

又 ， ，即 ，

因为 ，所以 ，

故 ，

因为 ，

所以 ，所以 ．

B．因为 ,

所以 ,

由 ，得 ，

所以 ．

C．因为曲线的极坐标方程，所以，即曲线 的直角坐标方程为 ，

将直线的参数方程为，代入抛物线方程，

得，即，

解得， ，

所以．

D．证明：因为都是正数，

所以，

，

又，所以，

当且仅当时等号成立．