题目内容
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,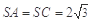 ,
,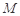 、
、 分别为
分别为 、
、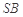 的中点.
的中点.

(1)求二面角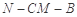 的余弦值;
的余弦值;
(2)求点 到平面
到平面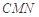 的距离.
的距离.
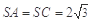 ,
,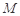 、
、 分别为
分别为 、
、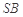 的中点.
的中点.
(1)求二面角
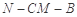 的余弦值;
的余弦值;(2)求点
 到平面
到平面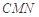 的距离.
的距离.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)本题中取
 中点
中点 ,将会出现许多垂直,这正是我们解题时需要的结果,由于
,将会出现许多垂直,这正是我们解题时需要的结果,由于 ,则
,则 ,由于平面
,由于平面 平面
平面 ,则
,则
 平面
平面 ,
,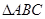 是正三角形,则
是正三角形,则 ,有了这些垂直后,就可以建立空间直角坐标系(以
,有了这些垂直后,就可以建立空间直角坐标系(以 为原点,
为原点, 分别为
分别为 轴),写出相应点的坐标,计算所需向量的坐标,设
轴),写出相应点的坐标,计算所需向量的坐标,设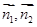 分别是二面角的两个面的法向量,则二面角的余弦值,就等于
分别是二面角的两个面的法向量,则二面角的余弦值,就等于 (或者其相反数,这要通过图形观察确定);(2)设平面
(或者其相反数,这要通过图形观察确定);(2)设平面 的法向量是
的法向量是 ,则点
,则点 以平面
以平面 的距离为
的距离为 .
.试题解析:⑴取
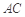 中点
中点 ,连结
,连结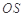 ?
? .∵
.∵ ,
, ,
,∴
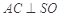 ,
, .∵平面
.∵平面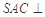 平面
平面 ,
,平面
 平面
平面 ,∴
,∴ 平面
平面 ,∴
,∴ .
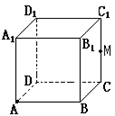
. 如图所示建立空间直角坐标系
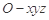 ,则
,则 ,
, ,
, ,
,∴
 .
.
∴
 .
.设
 为平面
为平面 的一个法向量,
的一个法向量,则
 ,
,取
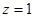 ,则
,则 ,∴
,∴ ,
,又
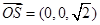 为平面
为平面 的一个法向量,
的一个法向量, ,即二面角
,即二面角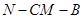 的余弦值为
的余弦值为 .
.(2)由⑴得
 ,又
,又 为平面
为平面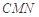 的一个法向量,
的一个法向量,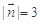 ,
,∴点
 到平面
到平面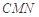 的距离
的距离 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
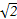
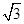 ,则k=( )
,则k=( )
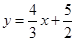 的距离为( )
的距离为( )
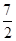
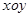 平面上的射影,则等于( )
平面上的射影,则等于( )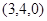
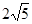
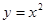 上的任意一点到直线
上的任意一点到直线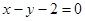 的最短距离为( )
的最短距离为( )

