Question

【题目】在△ABC中，三内角A，B，C满足．

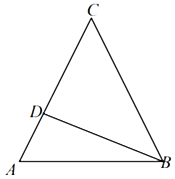
（Ⅰ）判断△ABC的形状；

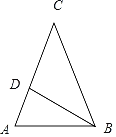
（Ⅱ）若点D在线段AC上，且CD＝2DA，，求tanA的值．

Answer 1

【答案】（Ⅰ）△ABC的形状为等腰三角形；（Ⅱ）tanA＝2．

【解析】

（Ⅰ）由已知利用三角函数恒等变换的应用化简可得cos（A﹣B）＝1，结合范围A﹣B∈（﹣π，π），可得A＝B，即可判断△ABC的形状为等腰三角形；

（Ⅱ）设DA＝x，CD＝2x，∠ABD＝θ，在△ADB，△CDB中，由正弦定理可得，利用三角函数恒等变换的应用可求tanA＝5tanθ，结合tanθ，可求tanA的值．

解：（Ⅰ）∵，

∴sinAsinB＝1﹣sin2cos2，

∴2sinAsinB＝1+cosC，

∵C＝π﹣（A+B），

∴2sinAsinB＝1+cos[π﹣（A+B）]＝1﹣cos（A+B），

∴2sinAsinB＝1﹣cosAcosB+sinAsinB，

即cosAcosB+sinAsinB＝1，即cos（A﹣B）＝1，

∵A﹣B∈（﹣π，π），

∴A﹣B＝0，可得A＝B，可得△ABC的形状为等腰三角形；

（Ⅱ）设DA＝x，CD＝2x，∠ABD＝θ，

在△ADB中，由正弦定理可得，即，

在△CDB中，由正弦定理可得，

即，即，

∴，

∴sin（A﹣θ）＝4cosAsinθ，

∴sinAcosθ﹣cosAsinθ＝4cosAsinθ，

∴sinAcosθ＝5cosAsinθ，

∴tanA＝5tanθ，

∵tanθ，

∴tanA＝2．