题目内容
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)A(不等式选做题)如果关于x的不等式|x-3|-|x-4|<a的解集不是空集,则实数a的取值范围是 ;
B(几何证明选做题)如图,圆O的割线PBA过圆心O,弦CD交AB于点E,且△COE~△PDE,PB=OA=2,则PE的长等于 ;
C(极坐标系与参数方程选做题)圆ρ=2COSθ的圆心到直线
 (t为参数)的距离是 .
(t为参数)的距离是 .
【答案】分析:A、先求不等式|x-3|+|x-4|的最大值,要求解集不是空集时实数a的取值范围,只要a大于不等式|x-3|+|x-4|的最大值即可.
B分析:、由已知中OA=2,我们可得圆的半径为2,由相交弦定理及三角形相似的性质,我们可以得到AF•BF=OF•PF,结合PB=OA=2,求出BF长,进而即可求出PF的长.
C、把极坐标方程和参数方程化为普通方程,利用点到直线的距离公式求出圆心到直线的距离.
解答:解:A、|x-3|+|x-4|的几何意义是数轴上的点x 到3和4的距离之差,
当x在3的左侧时,这个距离和最小值为-1.其它情况都大于-1
所以|x-3|-|x-4|≥-1
如果不是空集,所以 a>-1
故答案为:a>-1.
B、∵PB=OA=2,
∴OC=OB=2
由相交弦定理得:DF•CF=AF•BF
又∵△COF∽△PDF,
∴DF•CF=OF•PF
即AF•BF=OF•PF
即(4-BF)•BF=(2-BF)•(2+BF)
解得BF=1
故PF=PB+BF=3
故答案为:3.
C、圆ρ=2cosθ 即 (x-1)2+y2=1,表示以(1,0)为圆心,以1为半径的圆.
直线 (t为参数)即
(t为参数)即 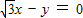 ,d=
,d=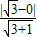 =
=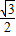 ,
,
故答案为: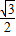 .
.
点评:本题A题考查绝对值不等式的几何意义,是基础题;B题点评:考查的知识点是相交弦定理及相似三角形的性质,其中根据相交弦定理及三角形相似的性质,得到AF•BF=OF•PF,是解答本题的关键;C题考查把极坐标方程和参数方程化为普通方程的方法,点到直线的距离公式的应用,将参数方程化为普通方程是解答关键.
B分析:、由已知中OA=2,我们可得圆的半径为2,由相交弦定理及三角形相似的性质,我们可以得到AF•BF=OF•PF,结合PB=OA=2,求出BF长,进而即可求出PF的长.
C、把极坐标方程和参数方程化为普通方程,利用点到直线的距离公式求出圆心到直线的距离.
解答:解:A、|x-3|+|x-4|的几何意义是数轴上的点x 到3和4的距离之差,
当x在3的左侧时,这个距离和最小值为-1.其它情况都大于-1
所以|x-3|-|x-4|≥-1
如果不是空集,所以 a>-1
故答案为:a>-1.
B、∵PB=OA=2,
∴OC=OB=2
由相交弦定理得:DF•CF=AF•BF
又∵△COF∽△PDF,
∴DF•CF=OF•PF
即AF•BF=OF•PF
即(4-BF)•BF=(2-BF)•(2+BF)
解得BF=1
故PF=PB+BF=3
故答案为:3.
C、圆ρ=2cosθ 即 (x-1)2+y2=1,表示以(1,0)为圆心,以1为半径的圆.
直线
 (t为参数)即
(t为参数)即 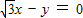 ,d=
,d=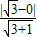 =
=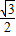 ,
,故答案为:
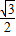 .
.点评:本题A题考查绝对值不等式的几何意义,是基础题;B题点评:考查的知识点是相交弦定理及相似三角形的性质,其中根据相交弦定理及三角形相似的性质,得到AF•BF=OF•PF,是解答本题的关键;C题考查把极坐标方程和参数方程化为普通方程的方法,点到直线的距离公式的应用,将参数方程化为普通方程是解答关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)