题目内容
【题目】已知a>0,a≠1.设命题p:函数y=loga(x+1)在(0,+∞)内单调递减;命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.若p或q为真,p且q为假,求a的取值范围.
【答案】![]()
【解析】试题分析:当![]() 为真命题时,根据对数型函数单调性的规律得到
为真命题时,根据对数型函数单调性的规律得到![]() ;根据一元二次方程根的判别式,得到当
;根据一元二次方程根的判别式,得到当![]() 为真命题时,
为真命题时, ![]() 或
或![]() ,因为“
,因为“![]() ”为真且“
”为真且“![]() ”为假,说明命题
”为假,说明命题![]() 、
、![]() 中一个为真,另一个为假,最后据此进行分类讨论,可得
中一个为真,另一个为假,最后据此进行分类讨论,可得![]() 的取值范围.
的取值范围.
试题解析:当![]() 时,函数
时,函数![]() 在
在![]() 内单调递减,当
内单调递减,当![]() 时,
时, ![]() 在
在![]() 内不是单调递减函数,故
内不是单调递减函数,故![]() 真时,
真时, ![]() ,
, ![]() 为真等价于
为真等价于![]() ,即
,即![]() 或
或![]() ,∵
,∵![]() 或
或![]() 为真,
为真, ![]() 且
且![]() 为假,∴
为假,∴![]() ,
, ![]() 中必定是一个为真一个为假.(1)若
中必定是一个为真一个为假.(1)若![]() 真,
真, ![]() 假时,则
假时,则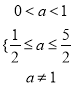 ,即
,即![]() ,(2)若
,(2)若![]() 假,
假, ![]() 真时,则
真时,则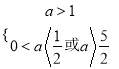 ,∴
,∴![]() ,综上可知,
,综上可知, ![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目