题目内容
9.已知2cos2α+3cosαsinα-3sin2α=1,α∈(-$\frac{3π}{2}$,-π),求:(1)tanα;
(2)$\frac{2sinα-3cosα}{4sinα-9cosα}$.
分析 (1)由已知得cos2α+3cosαsinα-4sin2α=0,两边同时除以cos2α,得到1+3tanα-4tan2α=0,由此能求出tanα.
(2)把$\frac{2sinα-3cosα}{4sinα-9cosα}$分子分母同时除以cosα,得到$\frac{2-3tanα}{4tanα-9}$,由此能求出结果.
解答 解:∵2cos2α+3cosαsinα-3sin2α=1,α∈(-$\frac{3π}{2}$,-π),
∴cos2α+3cosαsinα-4sin2α=0,
∴1+3tanα-4tan2α=0,
解得tanα=1(舍)或tanα=-$\frac{1}{4}$.
∴tanα=-$\frac{1}{4}$.
(2)$\frac{2sinα-3cosα}{4sinα-9cosα}$
=$\frac{2-3tanα}{4tanα-9}$
=$\frac{2-3×(-\frac{1}{4})}{4×(-\frac{1}{4})-9}$
=-$\frac{11}{40}$.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意同角三角函数关系式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列函数中,以π为周期的函数是( )
| A. | y=|sinx| | B. | y=sin|x| | C. | y=sinx | D. | y=$\frac{1}{2}$sinx |
14.在等差数列{an}中,a9=$\frac{1}{2}$a12+6,a2=4,设数列{an}的前n项和为Sn,则数列{$\frac{1}{{S}_{n}}$}的前10项和为( )
| A. | $\frac{11}{12}$ | B. | $\frac{10}{11}$ | C. | $\frac{9}{10}$ | D. | $\frac{8}{9}$ |
18.若A={x|x2-4=0},B={-1,0},则A∪B=( )
| A. | A | B. | ∅ | C. | B | D. | {-2,-1,0,2} |
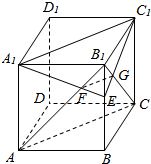 如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.
如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G. 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上.
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上.