题目内容
14.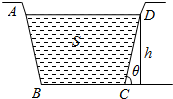 如图,水渠的横断面为等腰梯形,水的横断面面积为S,水面高为h,问侧面与地面所成角θ为多大时,横断面被水浸湿的长度(称为湿周)最小?并求出最小湿周.
如图,水渠的横断面为等腰梯形,水的横断面面积为S,水面高为h,问侧面与地面所成角θ为多大时,横断面被水浸湿的长度(称为湿周)最小?并求出最小湿周.
分析 设横断面被水浸湿的长度为l,AB=CD=x,可得l=$\frac{S}{h}$-(2-cosθ)•$\frac{h}{sinθ}$,导数法求到唯一的极值即为所求.
解答 解:设横断面被水浸湿的长度为l,AB=CD=x,
则l=BC+2x=$\frac{S}{h}$-xcosθ+2x=$\frac{S}{h}$-(2-cosθ)x
=$\frac{S}{h}$-(2-cosθ)•$\frac{h}{sinθ}$,
令l′=0,即$\frac{1-2cosθ}{si{n}^{2}θ}$,解得cosθ=$\frac{1}{2}$,θ=60°,
∵l只有1个极值点,也是最小值点,
把θ=60°代入l=$\frac{S}{h}$-(2-cosθ)•$\frac{h}{sinθ}$可得lmin=$\frac{S}{h}$+$\sqrt{3}$h,
∴当侧面与地面所成角θ=60°时,横断面被水浸湿的长度最小,且最小值为lmin=$\frac{S}{h}$+$\sqrt{3}$h,
点评 本题考查三角函数的最值,涉及三角形的边角关系和函数的极值,属中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
2.设函数f(x)=ln(x-1),则x•f(x)>1是x2•f(x)>1的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.已知非常数列且各项为正数等比数列{an}中,则( )
| A. | a1+a2014>a1007+a1008 | B. | a1+a2014<a1007+a1008 | ||
| C. | a1+a2014≥a1007+a1008 | D. | a1+a2014与a1007+a1008无法比较 |
6.求点P(-5,7)到直线12x+5y-3=0的距离( )
| A. | 1 | B. | 0 | C. | $\frac{14}{13}$ | D. | $\frac{28}{13}$ |