题目内容
19.求证:(x2+y2-4y-6)+λ(x2+y2-5x+y-6)=0恒过两定点.分析 由圆系方程可知(x2+y2-4y-6)+λ(x2+y2-5x+y-6)=0恒过两圆x2+y2-4y-6=0,x2+y2-5x+y-6=0的交点,联立方程组得答案.
解答 证明:由(x2+y2-4y-6)+λ(x2+y2-5x+y-6)=0,
联立$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-4y-6=0}\\{{x}^{2}+{y}^{2}-5x+y-6=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ 或$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$.
∴(x2+y2-4y-6)+λ(x2+y2-5x+y-6)=0恒过两定点(-1,-1),(3,3).
点评 本题考查圆系方程,考查方程组的解法,是基础题目.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
7.直线x+y=1与直线y=-2x+1的交点坐标是( )
| A. | (1,0) | B. | (0,1) | C. | (-1,0) | D. | (0,-1) |
9.下列各组函数中,表示同一函数的是( )
| A. | f(x)=$\root{5}{{x}^{5}}$与f(x)=$\sqrt{{x}^{2}}$ | B. | y=x与$y=\root{3}{x^3}$ | ||
| C. | $y=\frac{(x-1)(x+3)}{x-1}$与y=x+3 | D. | y=1与y=x0 |
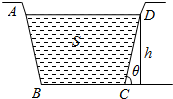 如图,水渠的横断面为等腰梯形,水的横断面面积为S,水面高为h,问侧面与地面所成角θ为多大时,横断面被水浸湿的长度(称为湿周)最小?并求出最小湿周.
如图,水渠的横断面为等腰梯形,水的横断面面积为S,水面高为h,问侧面与地面所成角θ为多大时,横断面被水浸湿的长度(称为湿周)最小?并求出最小湿周.