题目内容
2.设函数f(x)=ln(x-1),则x•f(x)>1是x2•f(x)>1的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 令g(x)=x•f(x)-1=xln(x-1)-1,(x>1).h(x)=x2•f(x)-1=x2ln(x-1)-1.(x>1).取x=3,2,即可判断出关系.
解答 解:令g(x)=x•f(x)-1=xln(x-1)-1,(x>1).h(x)=x2•f(x)-1=x2ln(x-1)-1.(x>1).
取x=3,则g(3)=3ln2-1>0,可得h(3)=9ln2-1>0.
反之不成立,取x=2.4,则h(2.4)>0,而g(2.4)<0.
因此x•f(x)>1是x2•f(x)>1的充分不必要条件.
故选:A.
点评 本题考查了充要条件的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.直线x+y=1与直线y=-2x+1的交点坐标是( )
| A. | (1,0) | B. | (0,1) | C. | (-1,0) | D. | (0,-1) |
12.已知命题p:“?x>0,有ex≥1成立,则¬p为( )
| A. | ?x0≤0,有ex0<l成立 | B. | ?x0≤0,有ex0≥1成立 | ||
| C. | ?x0>0,有ex0<1成立 | D. | ?x0>0,有ex0≤l成立 |
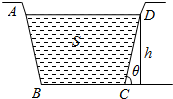 如图,水渠的横断面为等腰梯形,水的横断面面积为S,水面高为h,问侧面与地面所成角θ为多大时,横断面被水浸湿的长度(称为湿周)最小?并求出最小湿周.
如图,水渠的横断面为等腰梯形,水的横断面面积为S,水面高为h,问侧面与地面所成角θ为多大时,横断面被水浸湿的长度(称为湿周)最小?并求出最小湿周.