题目内容
18.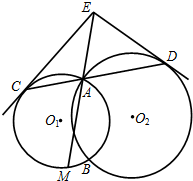 如图⊙O1与⊙O2相交于A、B两点,过A点的直线分别与⊙O1、⊙O2相文于C、D两点,以C、D为切点分别作两圆的切线相交于点E.
如图⊙O1与⊙O2相交于A、B两点,过A点的直线分别与⊙O1、⊙O2相文于C、D两点,以C、D为切点分别作两圆的切线相交于点E.(Ⅰ)若EA的延长线与⊙O1交于点M,证明切割线定理:EC2=EA•EM
(Ⅱ)证明:E、C、B、D四点共圆.
分析 (I)连结CM,利用EC是⊙O1切线,可证明△ECA~△EAC,推出EC2=EA•EM;
(II)连结CB、DB,证明∠ECA=∠CBA,得到∠EDA=∠DBA,然后证明E、C、B、D四点共圆.
解答 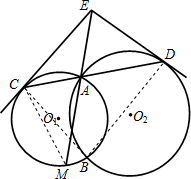 证明:(I)连结CM,∵EC是⊙O1切线,∴∠ECA=∠EMC,
证明:(I)连结CM,∵EC是⊙O1切线,∴∠ECA=∠EMC,
∵∠CEM=∠AEC,∴△ECA~△EAC,
∴$\frac{EC}{EM}=\frac{EA}{EC}$,∴EC2=EA•EM;…(5分)
(II)连结CB、DB,∵EC是⊙O1在C点的切线,
∴∠ECA=∠CBA,同理∠EDA=∠DBA,
∴∠DEC+∠CBD=∠DEC+(∠CBA+∠DBA)=∠DEC+(∠ECA+∠EDA)=180°,
∴E、C、B、D四点共圆.…(10分)
点评 本题考查三角形相似,圆的切线,四点共圆的判断,考查推理能力.

练习册系列答案
相关题目
6.已知(1+$\frac{2}{i}$)2=a+bi(a,b∈R,i为虚数单位),则a+b=( )
| A. | -7 | B. | 7 | C. | C-4 | D. | 4 |
13.把复数z的共轭复数记作$\overline{z}$,复数z=3-i(i为虚数单位),则复数$\frac{\overline{z}}{1+i}$在复平面内所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.设f(x)=$\left\{\begin{array}{l}{{k}^{2}x+{a}^{2}-k,(x≥0)}\\{{x}^{2}+({a}^{2}+4a)x+(3-a)^{2},(x<0)}\end{array}\right.$,其中a∈R,若对任意的非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x1)=f(x2)成立,则k的取值范围为( )
| A. | R | B. | [-4,0] | C. | [9,33] | D. | [-33,-9] |
6.“x<1”是“log${\;}_{\frac{1}{2}}}$x>0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |