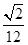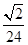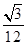题目内容
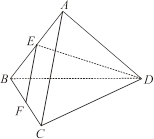
侧面都是直角三角形的正三棱锥,底面边长为a时,该三棱锥的全面积是( )
A.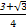 a2 a2 | B. a2 a2 |
C.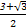 a2 a2 | D.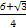 a2 a2 |
A
由于正三棱锥的侧面都是直角三角形,所以直角顶点应该就是棱锥的顶点,即棱锥的三条侧棱两两垂直,由于底面边长为a,所以侧棱长等于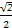 a,故该三棱锥的全面积S=
a,故该三棱锥的全面积S=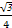 a2+3×
a2+3× ×(
×(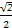 a)2=
a)2=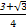 a2.故选A.
a2.故选A.
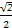 a,故该三棱锥的全面积S=
a,故该三棱锥的全面积S=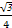 a2+3×
a2+3× ×(
×(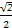 a)2=
a)2=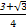 a2.故选A.
a2.故选A.
练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
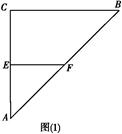
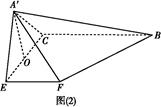
 A′BC的体积.
A′BC的体积.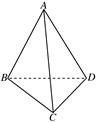
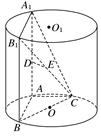
 的正方体
的正方体 中,点
中,点 和
和 分别是矩形
分别是矩形 和
和 的中心,则过点
的中心,则过点 、
、

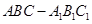 中,
中,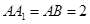 ,
,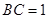 ,
,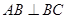 ,则该三棱柱的侧面积为 .
,则该三棱柱的侧面积为 .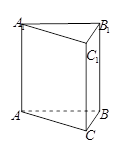
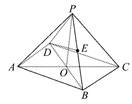
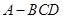 中,
中,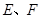 分别是
分别是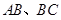 的中点,
的中点,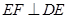 ,且
,且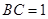 ,则正三棱锥
,则正三棱锥