题目内容
如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1,CB1的中点,DE⊥面CBB1.
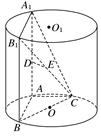
(1)证明:DE∥面ABC;
(2)求四棱锥CABB1A1与圆柱OO1的体积比.

(1)证明:DE∥面ABC;
(2)求四棱锥CABB1A1与圆柱OO1的体积比.
(1)见解析 (2)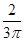
解:(1)证明:连接EO,OA.
∵E,O分别为B1C,BC的中点,
∴EO∥BB1.
又DA∥BB1,且DA=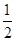 BB1=EO,
BB1=EO,
∴四边形AOED是平行四边形,
即DE∥OA.又DE?平面ABC,AO?平面ABC,
∴DE∥平面ABC.
(2)由题意知DE⊥平面CBB1,且由(1)知DE∥AO,
∴AO⊥平面CBB1,
∴AO⊥BC,
∴AC=AB.
∵BC是底面圆O的直径,
得CA⊥AB,且AA1⊥CA,
∴CA⊥平面AA1B1B,即CA为四棱锥CABB1A1的高.
设圆柱高为h,底面半径为r,
则VOO1=πr2h,V CABB1A1=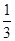 h(
h(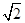 r)·(
r)·(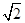 r)=
r)=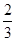 hr2.
hr2.
∴VCABB1A1∶V OO1=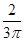 .
.
∵E,O分别为B1C,BC的中点,
∴EO∥BB1.
又DA∥BB1,且DA=
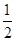 BB1=EO,
BB1=EO,∴四边形AOED是平行四边形,
即DE∥OA.又DE?平面ABC,AO?平面ABC,
∴DE∥平面ABC.
(2)由题意知DE⊥平面CBB1,且由(1)知DE∥AO,
∴AO⊥平面CBB1,
∴AO⊥BC,
∴AC=AB.
∵BC是底面圆O的直径,
得CA⊥AB,且AA1⊥CA,
∴CA⊥平面AA1B1B,即CA为四棱锥CABB1A1的高.
设圆柱高为h,底面半径为r,
则VOO1=πr2h,V CABB1A1=
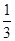 h(
h(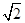 r)·(
r)·(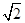 r)=
r)=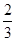 hr2.
hr2.∴VCABB1A1∶V OO1=
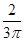 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
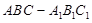 中,
中,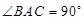 ,
,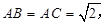
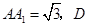 是
是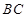 中点,
中点,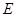 是
是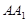 中点.
中点.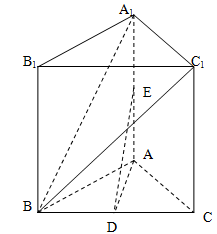
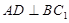 ;
;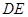 ∥面
∥面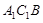 .
.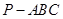 中,
中,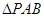 和
和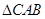 都是以
都是以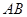 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,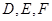 分别是
分别是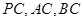 的中点.
的中点.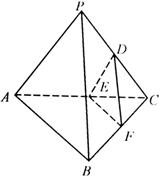
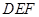 //平面
//平面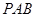 ;
;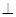
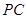 ;
;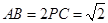 ,求三棱锥
,求三棱锥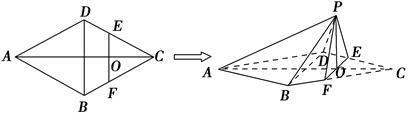
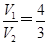 ,求此时线段PO的长.
,求此时线段PO的长.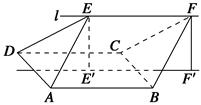
 中,底面
中,底面 为直角梯形,且
为直角梯形,且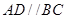 ,
, ,平面
,平面 底面
底面 为
为 的中点,
的中点, 是棱
是棱 的中点,
的中点, .
.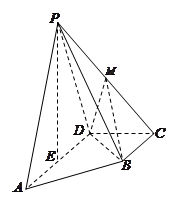

 平面
平面 ;
; 的体积.
的体积.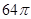


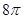
 A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A
A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A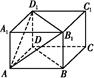
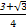 a2
a2 a2
a2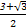 a2
a2 a2
a2