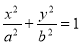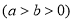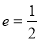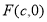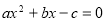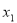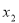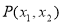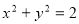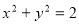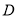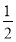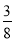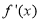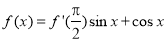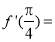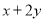题目内容
已知椭圆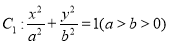 的离心率与双曲线
的离心率与双曲线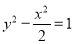 的离心率互为倒数,直线
的离心率互为倒数,直线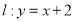 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆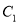 的方程;
的方程;
(2)设椭圆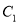 的左焦点为
的左焦点为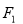 ,右焦点为
,右焦点为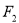 ,直线
,直线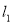 过点
过点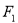 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线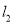 垂直
垂直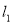 于点
于点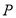 ,线段
,线段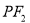 垂直平分线交
垂直平分线交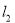 于点
于点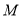 ,求点
,求点 的轨迹
的轨迹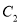 的方程;
的方程;
(3)设第(2)问中的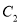 与
与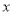 轴交于点
轴交于点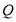 ,不同的两点
,不同的两点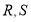 在
在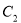 上,且满足
上,且满足 ,求
,求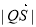 的取值范围.
的取值范围.
(1)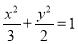 ;(2)
;(2)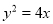 (3)
(3)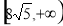
【解析】
试题分析:(1)双曲线的离心率为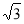 ,所以椭圆的离心率为
,所以椭圆的离心率为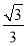 。根据题意原点到直线
。根据题意原点到直线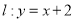 的距离为
的距离为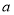 ,又因为
,又因为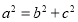 可解得
可解得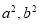 。(2)由题意知
。(2)由题意知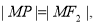 即点
即点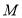 到直线
到直线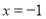 ,和到点
,和到点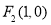 的距离相等,根据椭圆的定义可知点
的距离相等,根据椭圆的定义可知点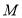 的轨迹是以
的轨迹是以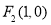 为焦点以直线
为焦点以直线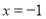 为准线的抛物线。(3)由
为准线的抛物线。(3)由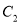 的方程为
的方程为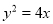 知
知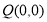 设
设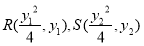 ,根据
,根据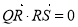 得出
得出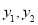 的关系,用两点间距离求
的关系,用两点间距离求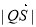 ,再用配方法求最值。
,再用配方法求最值。
试题解析:解(1)易知:双曲线的离心率为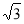 ,
,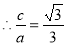 ,
,
即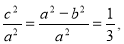
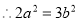 , 1分
, 1分
又由题意知: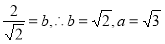 , 2分
, 2分
 椭圆
椭圆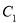 的方程为
的方程为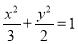 . 3分
. 3分
(2)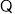
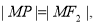
 动点
动点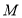 到定直线
到定直线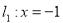 的距离等于它到定点
的距离等于它到定点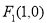 的距离 5分
的距离 5分
 动点
动点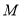 的轨迹
的轨迹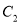 是以
是以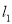 为准线,
为准线,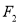 为焦点的抛物线, 6分
为焦点的抛物线, 6分
 点
点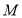 的轨迹
的轨迹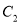 的方程为
的方程为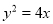 . 7分
. 7分
(3)由(2)知: ,设
,设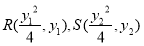 ,
,
则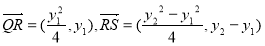 , 8分
, 8分
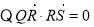
 , 9分
, 9分
由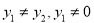 ,左式可化简为:
,左式可化简为: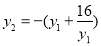 , 10分
, 10分
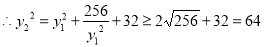 ,
,
当且仅当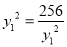 ,即
,即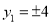 时取等号, 11分
时取等号, 11分
又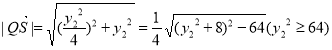 ,
,
 当
当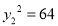 ,即
,即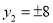 时,
时,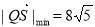 , 13分
, 13分
故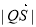 的取值范围是
的取值范围是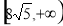 . 14分
. 14分
考点:1椭圆的标准方程;2抛物线的定义;3函数值域。