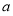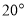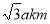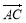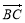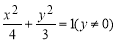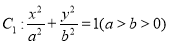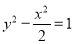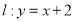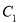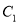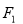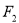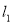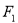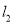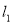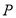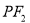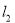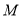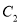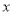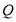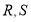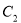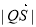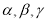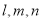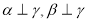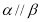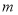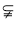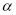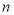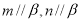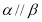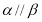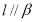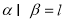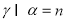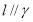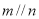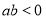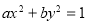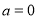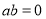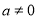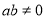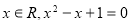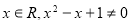题目内容
已知离心率为 的椭圆
的椭圆 (
( ) 过点
) 过点
(1)求椭圆 的方程;
的方程;
(2)过点 作斜率为
作斜率为 直线
直线 与椭圆相交于
与椭圆相交于 两点,求
两点,求 的长.
的长.
(1) 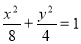 ;(2)
;(2) 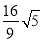
【解析】
试题分析:(1)将点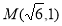 代入椭圆方程,结合离心率公式
代入椭圆方程,结合离心率公式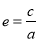 和
和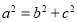 解方程组可得
解方程组可得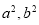 。(2)将直线和椭圆方程联立,消去
。(2)将直线和椭圆方程联立,消去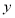 整理为关于
整理为关于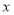 的一元二次方程,根据韦达定理得根与系数的关系。根据弦长公式可求其弦长。也可将上式一元二次方程求根,用两点间距离求弦长。
的一元二次方程,根据韦达定理得根与系数的关系。根据弦长公式可求其弦长。也可将上式一元二次方程求根,用两点间距离求弦长。
试题解析:【解析】
(1)由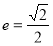 ,可得
,可得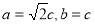 , 2分
, 2分
所以椭圆方程为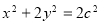
又椭圆过点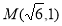 ,所以
,所以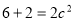 , 4分
, 4分
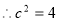 5分
5分
所以椭圆方程为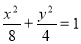 6分
6分
(2)由已知,直线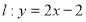 联立
联立 整理为
整理为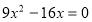 8分
8分
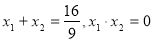 10分
10分
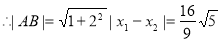 12分
12分
或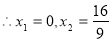 ,经计算
,经计算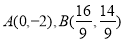 10分
10分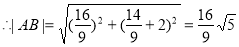 12分
12分
考点:1椭圆方程;2直线和椭圆相交弦问题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目