题目内容
【题目】已知函数![]() (
(![]() 且
且![]() ),
),![]()
(1)若![]() ,且函数
,且函数![]() 的值域为
的值域为![]() ,求
,求![]() 的解析式;
的解析式;
(2)在(1)的条件下,当![]() 时,
时,![]() 时单调函数,求实数
时单调函数,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() 时,若对于任意
时,若对于任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围
的取值范围
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)由函数![]() 的值域为
的值域为![]() ,得
,得![]() ,再结合
,再结合![]() ,从而求得
,从而求得![]() 的值,进而求得函数
的值,进而求得函数![]() 的解析式;
的解析式;
(2)函数![]() 的对称轴不在区间
的对称轴不在区间![]() 内即可;
内即可;
(3)将不等式![]() 恒成立转化为不等式组
恒成立转化为不等式组 对于任意
对于任意![]() ,
,![]() 恒成立,看成以
恒成立,看成以![]() 为主元,再分别研究两个不等式恒成立问题.
为主元,再分别研究两个不等式恒成立问题.
(1)函数![]() 的值域为
的值域为![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,解得:
,解得:![]()
所以![]() .
.
(2)因为![]()
![]() ,
,
对称轴为![]() ,
,
所以![]() 或
或![]() ,解得:
,解得:![]() 或
或![]() .
.
(3)当![]() 时,
时,![]() ,
,
因为![]()
![]()
![]() ,
,
所以不等式组 对于任意
对于任意![]() ,
,![]() 恒成立.
恒成立.
所以不等式组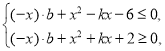 对于任意
对于任意![]() ,
,![]() 恒成立.
恒成立.
所以 对于任意
对于任意![]() 恒成立.
恒成立.
先考虑不等式![]() 对于任意
对于任意![]() 恒成立,所以
恒成立,所以![]() ;
;
再考虑不等式![]() 对于任意
对于任意![]() 恒成立(此时只考虑
恒成立(此时只考虑![]() 情况),
情况),
因为函数的对称轴为![]() ,
,
①当![]() 时,不等式
时,不等式![]() 对于任意
对于任意![]() 恒成立;
恒成立;
②当![]() 时,
时,![]() ,则
,则![]() ,
,
所以![]() ;
;
综上所述:![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目