题目内容
【题目】如果函数![]() 在定义域内存在区间[a,b],使
在定义域内存在区间[a,b],使![]() 在[a,b]上的值域是[2a,2b],那么称
在[a,b]上的值域是[2a,2b],那么称![]() 为“倍增函数”。
为“倍增函数”。
(I)判断![]() =
=![]() 是否为“倍增函数”,并说明理由;
是否为“倍增函数”,并说明理由;
(II)证明:函数![]() =
=![]() 是“倍增函数”;
是“倍增函数”;
(III)若函数![]() =ln(
=ln(![]() )是“倍增函数”,写出实数m的取值范围。(只需写出结论)
)是“倍增函数”,写出实数m的取值范围。(只需写出结论)
【答案】(I)见解析;(II)见证明;(III)![]() <m<0
<m<0
【解析】
(I)根据![]() 时,
时,![]() 判断出
判断出![]() 为“倍增函数”.(II)首先利用导数判断出
为“倍增函数”.(II)首先利用导数判断出![]() 为单调递增函数,构造函数
为单调递增函数,构造函数![]() ,利用导数求得函数
,利用导数求得函数![]() 有且只有两个零点,进而判断出函数
有且只有两个零点,进而判断出函数![]() 是“倍增函数”.(III)
是“倍增函数”.(III)![]() 为增函数,且
为增函数,且![]() 为“倍增函数”,所以
为“倍增函数”,所以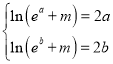 ,即
,即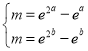 ;所以方程
;所以方程![]() ,化为
,化为![]() 有两个不相等的实数根,且两根都大于零.即
有两个不相等的实数根,且两根都大于零.即![]() ,解得
,解得![]() .所以
.所以![]() 的取值范围是
的取值范围是![]() .
.
解:(I)![]() =
=![]() 是“倍增函数”,理由如下:
是“倍增函数”,理由如下:
![]() =
=![]() 的定义域是R,且在[0,+
的定义域是R,且在[0,+![]() )上单调递增;
)上单调递增;
所以,当![]() [0,2]时,
[0,2]时,![]() ∈[0,4],
∈[0,4],
所以,![]() =
=![]() 是“倍增函数”。
是“倍增函数”。
(II)![]() =
=![]() 的定义域是R。
的定义域是R。
当x>0时,![]() =
=![]() >0,所以
>0,所以![]() 在区间(0,+
在区间(0,+![]() )上单调递增。
)上单调递增。
设![]() =
=![]() -2x=
-2x=![]() ,
,![]() =
=![]() 。
。
设h(x)=![]() =
=![]() ,
,![]() =
=![]() >0,
>0,
所以,h(x)在区间(-![]() ,+
,+![]() )上单调递增。
)上单调递增。
又h(0)=-2<0,h(1)=e-1>0,
所以,存在唯一的![]() ∈(0,1),使得h(
∈(0,1),使得h(![]() )=
)=![]() =0,
=0,
所以,当x变化时,![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:
x | (- |
| ( |
| - | 0 | + |
| ↘ | ↗ |
因为g(1)=e-3<0,g(2)=![]() >0,
>0,
所以,存在唯一的![]() ∈(1,2),使得
∈(1,2),使得![]() =0,
=0,
又![]() =0,所以函数
=0,所以函数![]() 只有两个零点,即0与
只有两个零点,即0与![]() 。
。
所以![]() =0,
=0,![]() =2
=2![]() 。
。
结合![]() 在区间(0,+
在区间(0,+![]() )上单调递增可知,当x∈[0,
)上单调递增可知,当x∈[0,![]() ]时
]时![]() 的值域是[0,2
的值域是[0,2![]() ]。
]。
所以,令[a,b]=[0,![]() ],
],![]() =
=![]() 是“倍增函数”。
是“倍增函数”。
(III)![]() <m<0。
<m<0。

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目




