题目内容
已知正四棱锥P-ABCD的底面边长及侧棱长均为13,M、N分别是PA、BD上的点,且PM:MA=BN:ND=5:8.(1)求证:直线MN∥平面PBC;
(2)求直线MN与平面ABCD所成的角.

【答案】分析:本题考查的知识点是直线与平面平行的判定,及线面夹角(1)要证明直线MN∥平面PBC,关键是在平面内找到可能与MN平行的直线,由已知我们根据平行线分线段成比例定理,及得结论;(2)要求直线MN与平面ABCD所成的角,即求直线PE与平面ABCD所成的角,构造三角形,解三角形即可求解.
解答:(1)证明:∵P-ABCD是正四棱锥,
∴ABCD是正方形.连接AN并延长交BC于点E,连接PE.
∵AD∥BC,∴EN:AN=BN:ND.
又∵BN:ND=PM:MA,
∴EN:AN=PM:MA.
∴MN∥PE.
又∵PE在平面PBC内,∴MN∥平面PBC.
(2)解:由(1)知MN∥PE,∴MN与平面ABCD所成的角就是PE与平面ABCD所成的角.
设点P在底面ABCD上的射影为O,连接OE,则∠PEO为PE与平面ABCD所成的角.
由正棱锥的性质知PO= =
= .
.
由(1)知,BE:AD=BN:ND=5:8,
∴BE= .
.
在△PEB中,∠PBE=60°,PB=13,BE= ,
,
根据余弦定理,得PE= .
.
在Rt△POE中,PO= ,PE=
,PE=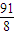 ,
,
∴sin∠PEO= =
= .
.
故MN与平面ABCD所成的角为arcsin .
.
点评:判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a?α,b?α,a∥b⇒a∥α);③利用面面平行的性质定理(α∥β,a?α⇒a∥β);④利用面面平行的性质(α∥β,a?α,a?,a∥α⇒?a∥β).线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.
解答:(1)证明:∵P-ABCD是正四棱锥,
∴ABCD是正方形.连接AN并延长交BC于点E,连接PE.
∵AD∥BC,∴EN:AN=BN:ND.
又∵BN:ND=PM:MA,
∴EN:AN=PM:MA.
∴MN∥PE.
又∵PE在平面PBC内,∴MN∥平面PBC.
(2)解:由(1)知MN∥PE,∴MN与平面ABCD所成的角就是PE与平面ABCD所成的角.
设点P在底面ABCD上的射影为O,连接OE,则∠PEO为PE与平面ABCD所成的角.
由正棱锥的性质知PO=
 =
= .
.由(1)知,BE:AD=BN:ND=5:8,
∴BE=
 .
.在△PEB中,∠PBE=60°,PB=13,BE=
 ,
,根据余弦定理,得PE=
 .
.在Rt△POE中,PO=
 ,PE=
,PE=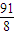 ,
,∴sin∠PEO=
 =
= .
.故MN与平面ABCD所成的角为arcsin
 .
.点评:判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a?α,b?α,a∥b⇒a∥α);③利用面面平行的性质定理(α∥β,a?α⇒a∥β);④利用面面平行的性质(α∥β,a?α,a?,a∥α⇒?a∥β).线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.

练习册系列答案
相关题目
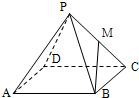
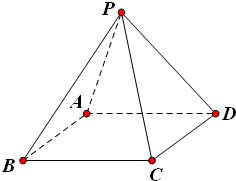 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h. ,M是侧棱PC的中点,则异面直线PA与BM所成角为 .
,M是侧棱PC的中点,则异面直线PA与BM所成角为 .