题目内容
顶点在原点,以坐标轴为对称轴的抛物线过点(-2,3),则它的方程是( )A.
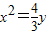
B.
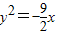
C.
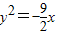 或
或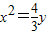
D.
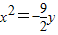 或
或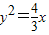
【答案】分析:对称轴分为是x轴和y轴两种情况,分别设出标准方程为y2=2px和x2=-2py,然后将M点坐标代入即可求出抛物线标准方程.
解答:解:(1)抛物线的顶点在坐标原点,对称轴是x轴,并且经过点 (-2,3),
设它的标准方程为y2=2px(p>0)
∴9=-4p,解得p=- ,
,
∴y2=- x.
x.
(2)抛物线的顶点在坐标原点,对称轴是y轴,并且经过点 (-2,3),
设它的标准方程为x2=-2py(p>0)
∴4=-6p,
解得:p= .
.
∴
故选C.
点评:本题考查了抛物线的标准方程,解题过程中要注意对称轴是x轴和y轴两种情况作答,属于基础题.
解答:解:(1)抛物线的顶点在坐标原点,对称轴是x轴,并且经过点 (-2,3),
设它的标准方程为y2=2px(p>0)
∴9=-4p,解得p=-
 ,
,∴y2=-
 x.
x.(2)抛物线的顶点在坐标原点,对称轴是y轴,并且经过点 (-2,3),
设它的标准方程为x2=-2py(p>0)
∴4=-6p,
解得:p=
 .
.∴

故选C.
点评:本题考查了抛物线的标准方程,解题过程中要注意对称轴是x轴和y轴两种情况作答,属于基础题.

练习册系列答案
相关题目
顶点在原点,以坐标轴为对称轴的抛物线过点(-2,3),则它的方程是( )
A、x2=
| ||||
B、y2=-
| ||||
C、y2=-
| ||||
D、x2=-
|