题目内容
已知正方形ABCD边长为a,将△ABD沿正方形的对角线BD所在的直线进行翻转,在翻转过程中,说法不正确的是( )
| A、将△ABD沿BD翻转到任意位置时,直线AC与直线BD都垂直 | ||||
| B、当平面ABD垂直于平面BCD时,此时∠ACD=60° | ||||
C、沿BD翻转到某个位置时,使得三棱锥A-BCD体积最大值是
| ||||
| D、沿BD翻转到任意位置时,三直线“AB与CD”,“AD与BC”,“AC与BD”均不垂直 |
分析:根据线面垂直的判定定理性质定理可判断A的正确性;根据二面角定义及通过计算可判断△ACD为正三角形;易知当平面ABD垂直于平面BCD时,该三棱锥高为OA最大,通过计算可求得三棱锥的最大体积;由A中结论即可判断D的正确性;
解答:解:如图所示:
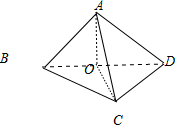
A中,由题意知,BD⊥OA,BD⊥OC,所以BD⊥平面OAC,故BD⊥AC,A正确;
B中,平面ABD垂直于平面BCD时,∠AOC为二面角A-BD-C的平面角,所以∠AOC=90°,则AC=
OA=
×
a=a,又AD=DC=a,所以△ACD为正三角形,故∠ACD=60°,B正确;
三棱锥A-BCD的底面为△BCD,面积为
a2,易知当平面ABD垂直于平面BCD时,该三棱锥高为OA最大,体积为
×
a2×OA=
×
a2×
a=
a3,C正确;
由A知将△ABD沿BD翻转到任意位置时,直线AC与直线BD都垂直,故D错误;
故选D.

A中,由题意知,BD⊥OA,BD⊥OC,所以BD⊥平面OAC,故BD⊥AC,A正确;
B中,平面ABD垂直于平面BCD时,∠AOC为二面角A-BD-C的平面角,所以∠AOC=90°,则AC=
| 2 |
| 2 |
| ||
| 2 |
三棱锥A-BCD的底面为△BCD,面积为
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 12 |
由A知将△ABD沿BD翻转到任意位置时,直线AC与直线BD都垂直,故D错误;
故选D.
点评:本题以命题为载体,考查空间中线线、线面、面面的位置关系及其判定、性质,考查学生空间想象能力.

练习册系列答案
相关题目
已知正方形ABCD边长为1,则|
+
+
|=( )
| AB |
| BC |
| AC |
| A、0 | ||
| B、2 | ||
C、
| ||
D、2
|
 已知正方形ABCD边长为1,图形如示,点E为边BC的中点,正方形内部一动点P满足:P到线段AD的距离等于P到点E的距离,那么P点的轨迹与正方形的上、下底边及BC边所围成平面图形的面积为
已知正方形ABCD边长为1,图形如示,点E为边BC的中点,正方形内部一动点P满足:P到线段AD的距离等于P到点E的距离,那么P点的轨迹与正方形的上、下底边及BC边所围成平面图形的面积为