题目内容
 已知正方形ABCD边长为1,图形如示,点E为边BC的中点,正方形内部一动点P满足:P到线段AD的距离等于P到点E的距离,那么P点的轨迹与正方形的上、下底边及BC边所围成平面图形的面积为
已知正方形ABCD边长为1,图形如示,点E为边BC的中点,正方形内部一动点P满足:P到线段AD的距离等于P到点E的距离,那么P点的轨迹与正方形的上、下底边及BC边所围成平面图形的面积为| 11 |
| 24 |
| 11 |
| 24 |
分析:由题设条件,需要先求出动点P的方程即抛物线的方程,再利用积分求出面积,积分时可以以x作为积分变量即可计算出两曲线所围成的图形的面积.
解答: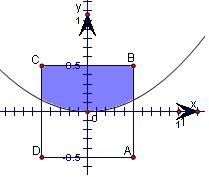 解:如图,建立平面直角坐标系,动点P的轨迹是以(0,
解:如图,建立平面直角坐标系,动点P的轨迹是以(0,
)为焦点的抛物线,其方程为:y=
x2,
那么P点的轨迹与正方形的上、下底边及BC边所围成平面图形的面积为
S=
(
-
x2)dx=(
x-
x3)
=
.
故答案为:
 解:如图,建立平面直角坐标系,动点P的轨迹是以(0,
解:如图,建立平面直角坐标系,动点P的轨迹是以(0,| 1 |
| 2 |
| 1 |
| 2 |
那么P点的轨迹与正方形的上、下底边及BC边所围成平面图形的面积为
S=
| ∫ |
-
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| | |
-
|
| 11 |
| 24 |
故答案为:
| 11 |
| 24 |
点评:本题考查抛物线的定义、抛物线的标准方程、定积分在求面积中的应用等基本知识,解答本题关键是确定积分变量与积分区间,有些类型的题积分时选择不同的积分变量,解题的难度是不一样的.

练习册系列答案
相关题目
已知正方形ABCD边长为1,则|
+
+
|=( )
| AB |
| BC |
| AC |
| A、0 | ||
| B、2 | ||
C、
| ||
D、2
|