题目内容
(本小题满分14分)设函数f(x) = x2 + bln(x+1),
(1)若对定义域的任意x,都有f(x)≥f(1)成立,求实数b的值;
(2)若函数f(x)在定义域上是单调函数,求实数b的取值范围;
(3)若b = -1,,证明对任意的正整数n,不等式 都成立
都成立
(1)b= - 4
(2)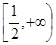
(3)略
【解析】解:(1)由x + 1>0得x> – 1∴f(x)的定义域为( - 1,+ ∞),
对x∈( - 1,+ ∞),都有f(x)≥f(1),
∴f(1)是函数f(x)的最小值,故有f/ (1) = 0,
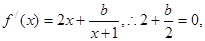
解得b= - 4.……………………………………………………………………4分
(2)∵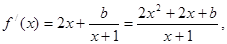
又函数f(x)在定义域上是单调函数,
∴f/ (x) ≥0或f/(x)≤0在( - 1,+ ∞)上恒成立。
若f/ (x) ≥0,∵x + 1>0,∴2x2 +2x+b≥0在( - 1,+ ∞)上恒成立,
即b≥-2x2 -2x = 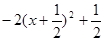 恒成立,由此得b≥
恒成立,由此得b≥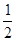 ;
;
若f/ (x) ≤0, ∵x + 1>0, ∴2x2 +2x+b≤0,即b≤-(2x2+2x)恒成立,
因-(2x2+2x) 在( - 1,+ ∞)上没有最小值,
∴不存在实数b使f(x) ≤0恒成立。
综上所述,实数b的取值范围是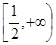 。………………………………8分
。………………………………8分
(3)当b= - 1时,函数f(x) = x2 - ln(x+1)
令函数h(x)=f(x) – x3 = x2 – ln(x+1) – x3,
则h/(x) = - 3x2 +2x - 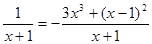 ,
,
∴当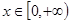 时,h/(x)<0所以函数h(x)在
时,h/(x)<0所以函数h(x)在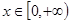 上是单调递减。
上是单调递减。
又h(0)=0,∴当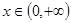 时,恒有h(x) <h(0)=0,
时,恒有h(x) <h(0)=0,
即x2 – ln(x+1) <x3恒成立.
故当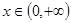 时,有f(x)
<x3..
时,有f(x)
<x3..
∵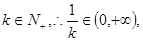
取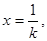 则有
则有
∴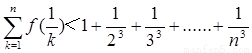 ,
,
故结论成立。………………………………………………………………14分

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)