题目内容
)已知某音响设备由五个部件组成,A电视机,B影碟机,C线路,D左声道和E右声道,其中每个部件工作的概率如图所示,能听到声音,当且仅当A与B中有一个工作,C工作,D与E中有一个工作;且若D和E同时工作则有立体声效果.
(1)求能听到立体声效果的概率;
(2)求听不到声音的概率.(结果精确到0.01)
(1)0.52;(2)0.13.
解析试题分析:(1)根据事件A,B,C,D,E 的能否正常工作没有影响,即是相互独立事件,又事件A发生的概率为0.9,由对立事件的概率得出事件A不发生的概率为1-0.90,同理事件B不发生的概率为1-0.8,根据独立事件的概率公式可得出能听到立体声效果的概率;(2)事件“听不到声音的”即为“当A、B都不工作,或C不工作,或D、E都不工作时”,又有独立事件的概率公式得出结论..
试题解析:(1)因为A与B中都不工作的概率为 ;
;
所以能听到立体声效果的概率为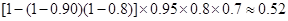 . 6分
. 6分
(2)当A、B都不工作,或C不工作,或D、E都不工作时,就听不到音响设备的声音.
其否定是:A、B至少有1个工作,且C工作,且D、E中至少有一个工作.
所以,听不到声音的概率为 .
.
10分
答:(1) 能听到立体声效果的概率约为0.52;(2)听不到声音的概率为0.13. 12分
考点:互斥事件、对立事件、独立事件的概率.

练习册系列答案
相关题目
某小组共有 、
、 、
、 、
、 、
、 五位同学,他们的身高(单位:米)以及体重指
五位同学,他们的身高(单位:米)以及体重指
标(单位:千克/米2)如下表所示:
| |  |  |  |  |  |
| 身高 |  |  |  |  |  |
| 体重指标 |  |  |  |  |  |
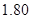 的同学中任选
的同学中任选 人,求选到的
人,求选到的 人身高都在
人身高都在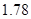 以下的概率;
以下的概率;(2)从该小组同学中任选
 人,求选到的
人,求选到的 人的身高都在
人的身高都在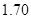 以上且体重指标都在
以上且体重指标都在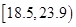 中的概率.
中的概率. 为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
| 高校 | 相关人数 | 抽取人数 |
| A | 18 |  |
| B | 36 | 2 |
| C | 54 | 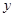 |
(1)求
 ,
,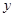 ;
;(2)若从高校B、C抽取的人中选2人作专题发言,
求这2人都来自高校C的概率.
 ,
, ,点
,点 的坐标为
的坐标为 .
. 时,点
时,点 的概率;
的概率; 时,点
时,点 顶点
顶点 起跳,每步从一顶点跳到相邻的顶点.
起跳,每步从一顶点跳到相邻的顶点.
 的概率
的概率 ;
; 表示跳到过
表示跳到过 .
.
 ,
,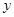 ;
; 人,求这2人都来自高二年级的概率.
人,求这2人都来自高二年级的概率. ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是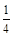 .
. 表示回答该题正确的人数,求
表示回答该题正确的人数,求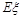 .
. 的概率分布列及期望.
的概率分布列及期望.