题目内容
【题目】曲线
的参数方程为
(
为参数)，以坐标原点为极点， 
轴的正半轴为极轴建立极坐标系，直线
的极坐标方程为
.
(1)写出
的直角坐标方程，并且用
(
为直线的倾斜角， 
为参数)的形式写出直线
的一个参数方程；
(2) 
与
是否相交，若相交求出两交点的距离，若不相交，请说明理由.
【答案】（1）
的直角坐标方程为
，直线
的一个参数方程为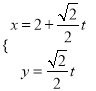
(
为参数)；（2）相交，且两交点的距离为
．
【解析】试题分析：
(1)由题意可得
的直角坐标方程为
，直线
的一个参数方程为
(
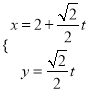为参数)；
(2)联立直线与椭圆的方程，很明显直线与椭圆有两个交点，且两交点的距离是
．
试题解析：
(1) 
的直角坐标方程为
，
由
得
，直线
的倾斜角为
，
过点
，故直线
的一个参数方程为
(
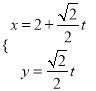为参数)
(2)将
的参数方程代入
的直角坐标方程得
， 
， 
，
显然
与
有两个交点
且
.
练习册系列答案
相关题目
【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机，买新机时，同时购买墨盒，每台新机随机购买第一盒墨150元，优惠0元；再每多买一盒墨都要在原优惠基础上多优惠一元，即第一盒墨没有优惠，第二盒墨优惠一元，第三盒墨优惠2元，……，依此类推，每台新机最多可随新机购买25盒墨．平时购买墨盒按零售每盒200元．
公司根据以往的记录，十台打印机正常工作五年消耗墨盒数如下表：
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
以这十台打印机消耗墨盒数的频率代替一台打印机消耗墨盒数发生的概率，记ξ表示两台打印机5年消耗的墨盒数．
(1)求ξ的分布列；
(2)若在购买两台新机时，每台机随机购买23盒墨，求这两台打印机正常使用五年在消耗墨盒上所需费用的期望．
