题目内容
 设全集U=R,A={x|x(-x-3)>0},B={x|y=ln(-x-1)},则如图中阴影部分表示的集合为( )
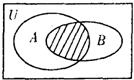
设全集U=R,A={x|x(-x-3)>0},B={x|y=ln(-x-1)},则如图中阴影部分表示的集合为( )分析:根据所给的文恩图,看出阴影部分所表达的是集合A和集合B的交集.
解答:解:由题意可知集合A中x必须满足x(-x-3)>0
即-3<x<0,
集合B中-x-1必须大于0
所以集合B中x必须满足x<-1,
图中阴影部分表示A∩B,
∴A∩B={x|-3<x<-1}
故选:C.
即-3<x<0,
集合B中-x-1必须大于0
所以集合B中x必须满足x<-1,
图中阴影部分表示A∩B,
∴A∩B={x|-3<x<-1}
故选:C.
点评:本题考查文恩图表达集合的关系及运算,本题解题的关键是正确读出文恩图,再计算出两个集合之间的交集.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
设全集U=R,A={x|ax+1=0},B={1,2},若A∩(?UB)=?,则实数a的取值集合是( )
| A、{0} | ||
| B、? | ||
C、{-1,-
| ||
D、{-1,-
|