题目内容
设全集U=R，A={x|| x-2 |
| x+1 |
| ||
| 2 |
分析：根据集合A中的不等式
＜0得到x-2与x+1异号，列出不等式求出解集即可得到集合A，再根据正弦函数的周期性与图象，利特殊角的三角函数值得到x的取值范围即可得到集合B，求出A与B的交集即可．
| x-2 |
| x+1 |
解答：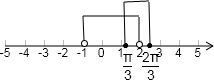
解：由A={x|
＜0}得到
＜0，
即
或
，解得-1＜x＜2；
根据正弦函数图象和周期性得到：2kπ+
＜x＜2kπ+
所以A=（-1，2），B={x|sinx≥
}=[2kπ+
，2kπ+
]（k∈Z）
把集合画在数轴上，如图，则A∩B=[
，2)．
故答案为：[
，2)
解：由A={x|| x-2 |
| x+1 |
| x-2 |
| x+1 |
即
|
|
根据正弦函数图象和周期性得到：2kπ+
| π |
| 3 |
| 2π |
| 3 |
所以A=（-1，2），B={x|sinx≥
| ||
| 2 |
| π |
| 3 |
| 2π |
| 3 |
把集合画在数轴上，如图，则A∩B=[
| π |
| 3 |
故答案为：[
| π |
| 3 |
点评：此题要求学生会根据正弦函数值的范围利用正弦函数的图象和周期性求出自变量的范围，掌握
＜0这种不等式的解法，以及会求两个集合的交集运算．
| x-a |
| x-b |
练习册系列答案
相关题目
设全集U=R，A={x|ax+1=0}，B={1，2}，若A∩（?UB）=?，则实数a的取值集合是（ ）
| A、{0} | ||
| B、? | ||
C、{-1，-
| ||
D、{-1，-
|