题目内容
(本小题满分14分)
已知F1，F2分别是椭圆＋＝1的左、右焦点，曲线C是以坐标原点为顶点，以F2为焦点的抛物线，自点F1引直线交曲线C于P、Q两个不同的交点，点P关于x轴的对称点记为M.设＝λ.
(Ⅰ)求曲线C的方程；
(Ⅱ)证明：＝－λ；
(Ⅲ)若λ∈[2,3]，求|PQ|的取值范围.
【答案】
解：(Ⅰ)∵椭圆＋＝1的右焦点F2的坐标为(1,0)，
∴可设曲线C的方程为y2＝2px.(p>0)
∴p＝2.
曲线C的方程为y2＝4x. (3分)
(Ⅱ)设P(x1，y1)，Q(x2，y2)，M(x1，－y1).
∵
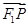＝λ
，
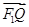∴x1＋1＝λ(x2＋1). ①
y1＝λy2， ②
∴y＝λ2y，
∵y＝4x1，y＝4x2.
∴x1＝λ2x2. ③
③代入①得λ2x2＋1＝λx2＋λ.
∴λx2(λ－1)＝λ－1.
∵λ≠1，∴x2＝，x1＝λ.
∴
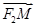＝(x1－1，－y1).
由②知，－y1＝－λy2，
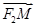∴＝－λ(－1，y2)，
＝－λ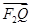
.
故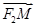＝－λ.
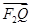(9分)
(Ⅲ)由(Ⅱ)知x2＝，x1＝λ，得x1x2＝1.
∴y·y＝16x1x2＝16.
∵y1y2>0，∴y1y2＝4.
则|PQ|2＝(x1－x2)2＋(y1－y2)2
＝x＋x＋y＋y－2(x1x2＋y1y2)
＝(λ＋)2＋4(λ＋)－12
＝(λ＋＋2)2－16.
∵λ∈[2,3]，∴λ＋∈.
∴|PQ|2∈.
得|PQ|∈.
【解析】略
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
(a＞b＞0)，曲线C2的方程为y=
，且曲线C1与C2在第一象限内只有一个公共点P。（1）试用a表示点P的坐标；（2）设A、B是椭圆C1的两个焦点，当a变化时，求△ABP的面积函数S(a)的值域；（3）记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积，试求函数f(a)=min{g(a), S(a)}的表达式。
=2，点（
）在函数
的图像上，其中
=
.
}是等比数列；
，求
及数列{
}的通项公式；
，求数列{
}的前n项和
，并证明
.
天(
)的销售价格(单位：元)为
，第
，已知该商品成本为每件25元.
关于第
的图像在点
处的切线与直线
平行.
，
满足的关系式；
上恒成立，求
（
）