题目内容
【题目】如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ. 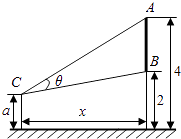
(1)若a=1.5,问:观察者离墙多远时,视角θ最大?
(2)若tanθ= ![]() ,当a变化时,求x的取值范围.
,当a变化时,求x的取值范围.
【答案】
(1)解:如图,作CD⊥AF于D,则CD=EF,
设∠ACD=α,∠BCD=β,CD=x,则θ=α﹣β,
在Rt△ACD和Rt△BCD中,tanα= ![]() ,tanβ=
,tanβ= ![]() ,
,
则tanθ=tan(α﹣β)= ![]() =
= ![]() (x>0),
(x>0),
令u= ![]() ,则ux2﹣2x+1.25u=0,
,则ux2﹣2x+1.25u=0,
∵上述方程有大于0的实数根,∴△≥0,
即4﹣4×1.25u2≥0,∴u≤ ![]() ,即(tanθ)max=
,即(tanθ)max= ![]() ,
,
∵正切函数y=tanx在(0, ![]() )上是增函数,
)上是增函数,
∴视角θ同时取得最大值,
此时,x= ![]() =
= ![]() ,
,
∴观察者离墙 ![]() 米远时,视角θ最大
米远时,视角θ最大

(2)解:由(1)可知,tanθ= ![]() =
= 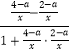 =
= ![]() ,
,
即x2﹣4x+4=﹣a2+6a﹣4,
∴(x﹣2)2=﹣(a﹣3)2+5,
∵1≤a≤2,
∴1≤(x﹣2)2≤4,
化简得:0≤x≤1或3≤x≤4,
又∵x>1,
∴3≤x≤4.
【解析】(1)首项利用两角和的正切公式建立函数关系,进一步利用判别式确定函数的最大值;(2)利用两角和的正切公式建立函数关系,利用a的取值范围即可确定x的范围.

【题目】某校在高三抽取了500名学生,记录了他们选修A、B、C三门课的选修情况,如表:
科目 学生人数 | A | B | C |
120 | 是 | 否 | 是 |
60 | 否 | 否 | 是 |
70 | 是 | 是 | 否 |
50 | 是 | 是 | 是 |
150 | 否 | 是 | 是 |
50 | 是 | 否 | 否 |
(Ⅰ)试估计该校高三学生在A、B、C三门选修课中同时选修2门课的概率.
(Ⅱ)若该高三某学生已选修A,则该学生同时选修B、C中哪门的可能性大?