题目内容
已知函数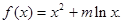 .
.
(1)若函数f(x)的图象在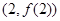 处的切线斜率为3,求实数m的值;
处的切线斜率为3,求实数m的值;
(2)求函数f(x)的单调区间;
(3)若函数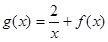 在[1,2]上是减函数,求实数m的取值范围.
在[1,2]上是减函数,求实数m的取值范围.
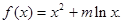 .
.(1)若函数f(x)的图象在
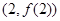 处的切线斜率为3,求实数m的值;
处的切线斜率为3,求实数m的值;(2)求函数f(x)的单调区间;
(3)若函数
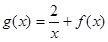 在[1,2]上是减函数,求实数m的取值范围.
在[1,2]上是减函数,求实数m的取值范围. 解:(1)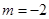 .
.
(2)函数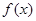 的单调递减区间是
的单调递减区间是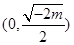 ;单调递增区间是
;单调递增区间是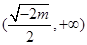 .
.
(3)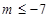 .
.
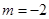 .
. (2)函数
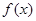 的单调递减区间是
的单调递减区间是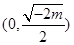 ;单调递增区间是
;单调递增区间是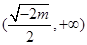 .
. (3)
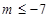 .
. 本题主要考查了函数的导数的求解,利用导数判断函数的单调区间,体现了分类讨论思想的应用,及函数的恒成立与函数的最值求解的相互转化思想的应用.
(Ⅰ)先对函数求导,然后由由已知f'(2)=1,可求a
(II)先求函数f(x)的定义域为(0,+∞),要判断函数的单调区间,需要判断导数f′(x)的正负,分类讨论:分(1)当a≥0时,(2)当a<0时两种情况分别求解
(II)由g(x)可求得g′(x),由已知函数g(x)为[1,2]上的单调减函数,可知g'(x)≤0在[1,2]上恒成立,即a≤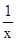 -x2在[1,2]上恒成立,要求a的范围,只要求解h(x)=
-x2在[1,2]上恒成立,要求a的范围,只要求解h(x)= 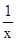 -x2,在[1,2]上的最小值即可
-x2,在[1,2]上的最小值即可
(Ⅰ)先对函数求导,然后由由已知f'(2)=1,可求a
(II)先求函数f(x)的定义域为(0,+∞),要判断函数的单调区间,需要判断导数f′(x)的正负,分类讨论:分(1)当a≥0时,(2)当a<0时两种情况分别求解
(II)由g(x)可求得g′(x),由已知函数g(x)为[1,2]上的单调减函数,可知g'(x)≤0在[1,2]上恒成立,即a≤
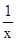 -x2在[1,2]上恒成立,要求a的范围,只要求解h(x)=
-x2在[1,2]上恒成立,要求a的范围,只要求解h(x)= 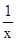 -x2,在[1,2]上的最小值即可
-x2,在[1,2]上的最小值即可
练习册系列答案
相关题目
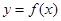 是定义在
是定义在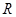 上的奇函数,当
上的奇函数,当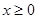 时,
时,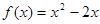 。
。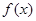 的解析式;
的解析式; 为何值时,方程
为何值时,方程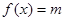 有三个解?
有三个解? 元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若
元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若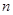 天购买一次,需要支付
天购买一次,需要支付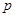 是多少元?[
是多少元?[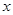 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这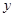 (元)关于
(元)关于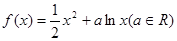 .
.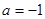 ,求
,求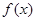 的单调递增区间;
的单调递增区间;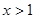 时,
时,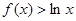 恒成立,求实数
恒成立,求实数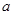 的取值范围.
的取值范围.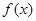 的定义域为
的定义域为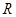 ,
,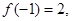 对任意
对任意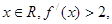 则
则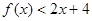 的解集为( )
的解集为( )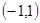
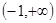
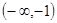
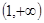
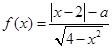 为奇函数,则
为奇函数,则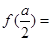 ( )
( )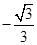
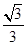
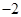
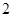
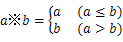 .如1※2=1,则函数
.如1※2=1,则函数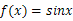 ※
※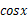 的值域为 .
的值域为 . 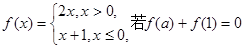 ,则a= 。
,则a= 。