题目内容
已知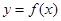 是定义在
是定义在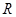 上的奇函数,当
上的奇函数,当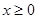 时,
时,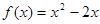 。
。
(1)求函数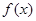 的解析式;
的解析式;
(2)画出函数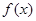 的图象,并求函数
的图象,并求函数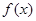 的单调区间;
的单调区间;
(3)当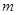 为何值时,方程
为何值时,方程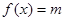 有三个解?
有三个解?
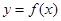 是定义在
是定义在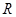 上的奇函数,当
上的奇函数,当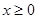 时,
时,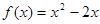 。
。(1)求函数
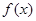 的解析式;
的解析式;(2)画出函数
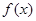 的图象,并求函数
的图象,并求函数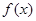 的单调区间;
的单调区间;(3)当
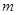 为何值时,方程
为何值时,方程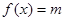 有三个解?
有三个解?解:(1)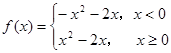
(2)
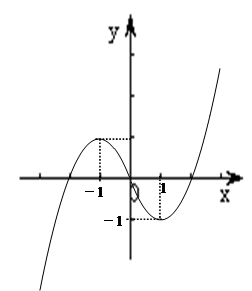
由图象可得函数的增区间是: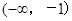 和
和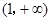 , 减区间是:
, 减区间是: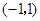
(3)由图象得:当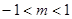 时,方程
时,方程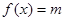 有三个解
有三个解
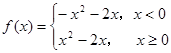
(2)

由图象可得函数的增区间是:
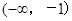 和
和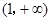 , 减区间是:
, 减区间是: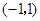
(3)由图象得:当
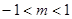 时,方程
时,方程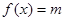 有三个解
有三个解 本试题主要是考查了函数的单调性以及函数的奇偶性的运用,以及函数的解析式的求解的综合运用。
(1)由题意设x>0利用已知的解析式求出f(-x)=x2+2x,再由f(x)=-f(-x),求出x>0时的解析式
(2)根据解析式作出函数的图像,并写出单调区间。
(3)要是方程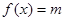 有三个解,那么利用常函数与图像的交点情况可以得到。
有三个解,那么利用常函数与图像的交点情况可以得到。
(1)由题意设x>0利用已知的解析式求出f(-x)=x2+2x,再由f(x)=-f(-x),求出x>0时的解析式
(2)根据解析式作出函数的图像,并写出单调区间。
(3)要是方程
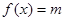 有三个解,那么利用常函数与图像的交点情况可以得到。
有三个解,那么利用常函数与图像的交点情况可以得到。
练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
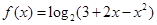 .
. 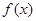 的定义域;
的定义域;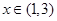 上是减函数;
上是减函数;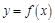 是
是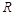 上的偶函数,且
上的偶函数,且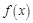 在
在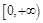 上是减函数,若
上是减函数,若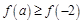 ,则
,则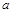 的取值范围是( )
的取值范围是( )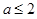
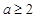
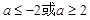
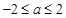
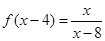 ,则函数
,则函数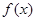 = ( )
= ( )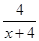
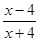
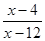
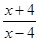
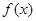 为定义在
为定义在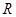 上的奇函数,当
上的奇函数,当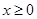 时,
时,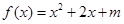 (
(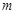 为常数),则
为常数),则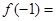 ;
;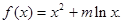 .
.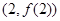 处的切线斜率为3,求实数m的值;
处的切线斜率为3,求实数m的值;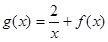 在[1,2]上是减函数,求实数m的取值范围.
在[1,2]上是减函数,求实数m的取值范围. 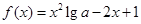 的图像与
的图像与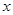 轴有两个交点,则实数
轴有两个交点,则实数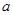 的取值范围是( )
的取值范围是( )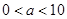 B.
B.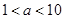 .
.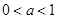 D.
D.