题目内容
已知
=(
sinx,cosx),
=(cosx,-cosx),x∈R,定义函数f(x)=
•
-
(1)求函数f(x)的最小正周期,值域,单调增区间.
(2)设△ABC的三内角A,B,C所对的边分别为a、b、c,且c=
,f(C)=0,若向量
=(1,sinA)与
=(2,sinB)共线,求边a,b的值及△ABC的面积S?
| m |
| 3 |
| n |
| m |
| n |
| 1 |
| 2 |
(1)求函数f(x)的最小正周期,值域,单调增区间.
(2)设△ABC的三内角A,B,C所对的边分别为a、b、c,且c=
| 3 |
| d |
| e |
分析:(1)利用向量的数量积的坐标表示及辅助角公式对已知函数进行化简,然后结合正弦函数的性质即可求解
(2)由f(C)=sin(2C-
)-1=0,及C为△ABC的内角,可求C,然后结合向量共线的坐标表示可得sinB与sinA的关系,根据正弦定理进而可得b与a的关系,最后利用余弦定理得:c2=a2+b2-2abcosC,即可求解
(2)由f(C)=sin(2C-
| π |
| 6 |
解答:解:(1)∵f(x)=
-
=
sinx•cosx-cos2x-
=
sin2x-
-
=sin(2x-
)-1
∴f(x)的最小正周期T=π,值域为[-2,0],
令2kπ2kπ-
≤2x+
≤2kπ+
⇒kπ+
≤x≤kπ+
,(k∈Z),
∴f(x)的增区间为:[kπ+
,kπ+
] (k∈Z),
(2)∵f(x)=sin(2x-
)-1,f(C)=0,
∴f(C)=sin(2C-
)-1=0,又C为△ABC的内角,
∴C=
又
=(1,sinA)与
=(2,sinB)共线
∴sinB=2sinA,根据正弦定理得:b=2a①,
由余弦定理得:c2=a2+b2-2abcosC,即3=a2+b2-ab②,
联立①②,解得a=1,b=2.
∴△ABC的面积S=
absinC=
| m• |
| n |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
∴f(x)的最小正周期T=π,值域为[-2,0],
令2kπ2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
∴f(x)的增区间为:[kπ+
| π |
| 6 |
| π |
| 3 |
(2)∵f(x)=sin(2x-
| π |
| 6 |
∴f(C)=sin(2C-
| π |
| 6 |
∴C=
| π |
| 3 |
又
| d |
| e |
∴sinB=2sinA,根据正弦定理得:b=2a①,
由余弦定理得:c2=a2+b2-2abcosC,即3=a2+b2-ab②,
联立①②,解得a=1,b=2.
∴△ABC的面积S=
| 1 |
| 2 |
| ||
| 2 |
点评:本题主要考查了向量数量积及向量平行的坐标表示的应用,二倍角公式、辅助角公式等公式在三角函数化简中的应用,正弦定理及余弦定理的综合应用,本题具有一定的综合性

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
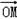 =(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为
=(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为 =(a,b)(其中O为坐标原点),记平面内所有向量的“相伴函数”构成的集合为S。
=(a,b)(其中O为坐标原点),记平面内所有向量的“相伴函数”构成的集合为S。 )+4sinx,求证:g(x)∈S;
)+4sinx,求证:g(x)∈S; 的“相伴函数”f(x)在x=x0处取得最大值,当点M在圆C上运动时,求tan2x0的取值范围。
的“相伴函数”f(x)在x=x0处取得最大值,当点M在圆C上运动时,求tan2x0的取值范围。 =(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为
=(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为 =(a,b)(其中O为坐标原点).记平面内所有向量的“相伴函数”构成的集合为S.
=(a,b)(其中O为坐标原点).记平面内所有向量的“相伴函数”构成的集合为S. )+4sinx,求证:g(x)∈S;
)+4sinx,求证:g(x)∈S; 的“相伴函数”f(x)在x=x处取得最大值.当点M在圆C上运动时,求tan2x的取值范围.
的“相伴函数”f(x)在x=x处取得最大值.当点M在圆C上运动时,求tan2x的取值范围.