题目内容
设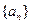 是由正数组成的比数列,
是由正数组成的比数列,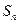 是其前
是其前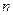 项和.
项和.
(1)证明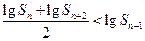 ;
;
(2)是否存在常数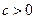 ,使得
,使得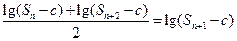 成立?并证明你的结论.
成立?并证明你的结论.
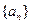 是由正数组成的比数列,
是由正数组成的比数列,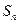 是其前
是其前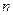 项和.
项和.(1)证明
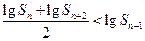 ;
;(2)是否存在常数
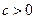 ,使得
,使得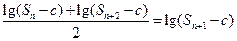 成立?并证明你的结论.
成立?并证明你的结论.(1)证明见答案(2)不存在
(1)证明:设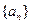 公比为
公比为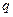 ,则已知
,则已知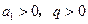 ;
;
当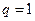 时,
时,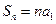 ,从而
,从而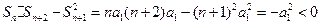 ;
;
当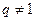 时,
时,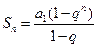 ,从而
,从而
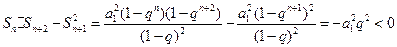 ,
,
得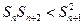 .
.
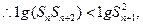 即
即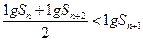 .
.
(2)解:不存在.
要使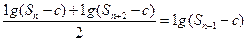 成立,则有
成立,则有
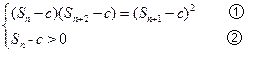
分两种情况讨论:
当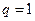 时,
时,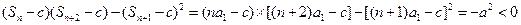
可知不满足条件①即不存在常数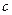 使结论成立.
使结论成立.
当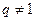 时,若条件①成立,
时,若条件①成立,
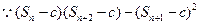
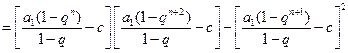
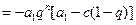 ,
,
且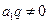 ,故只能有
,故只能有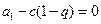 ,即
,即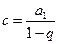 .
.
此时,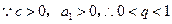 ,
,
但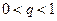 时,
时,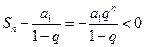 不满足条件②,即不存在常数
不满足条件②,即不存在常数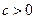 ,使结论成立.
,使结论成立.
综合以上知同时满足①,②的常数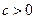 不存在,即不存在常数
不存在,即不存在常数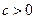 ,使
,使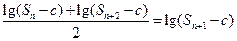 .
.
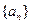 公比为
公比为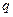 ,则已知
,则已知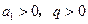 ;
;当
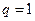 时,
时,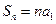 ,从而
,从而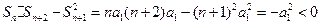 ;
;当
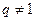 时,
时,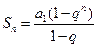 ,从而
,从而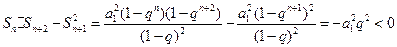 ,
,得
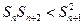 .
.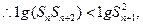 即
即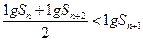 .
.(2)解:不存在.
要使
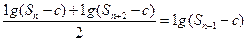 成立,则有
成立,则有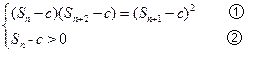
分两种情况讨论:
当
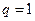 时,
时,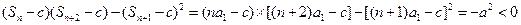
可知不满足条件①即不存在常数
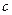 使结论成立.
使结论成立.当
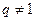 时,若条件①成立,
时,若条件①成立,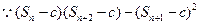
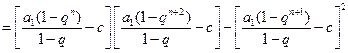
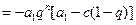 ,
,且
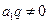 ,故只能有
,故只能有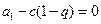 ,即
,即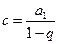 .
. 此时,
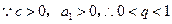 ,
,但
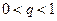 时,
时,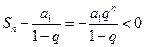 不满足条件②,即不存在常数
不满足条件②,即不存在常数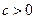 ,使结论成立.
,使结论成立.综合以上知同时满足①,②的常数
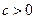 不存在,即不存在常数
不存在,即不存在常数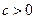 ,使
,使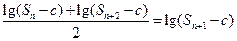 .
.
练习册系列答案
相关题目
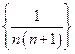 的前
的前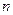 项和
项和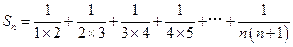 ,研究一下,能否找到求
,研究一下,能否找到求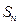 的一个公式.你能对这个问题作一些推广吗?
的一个公式.你能对这个问题作一些推广吗?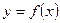 的图像经过坐标原点,且
的图像经过坐标原点,且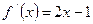 ,数列
,数列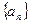 的前
的前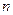 项和
项和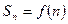
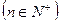
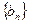 满足
满足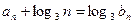 ,求数列
,求数列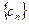 满足
满足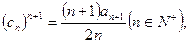 求数列
求数列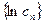 中的最大值。
中的最大值。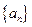 满足递推关系式:
满足递推关系式: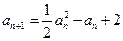 ,
,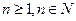 .
.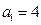 ,证明:(ⅰ)当
,证明:(ⅰ)当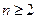 时,有
时,有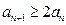 ;(ⅱ)当
;(ⅱ)当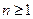 时,有
时,有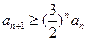 .
.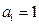 ,证明:当
,证明:当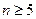 时,有
时,有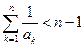 .
.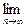 xn
xn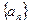 的前n项和为Sn,若
的前n项和为Sn,若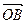 =a1
=a1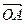 +a2008
+a2008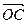 ,且A,B,C三点共线
,且A,B,C三点共线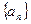 的各项均为正数,若
的各项均为正数,若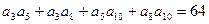 ,
,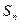 为
为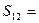 ______________。
______________。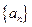 中,
中,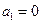 ,
,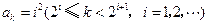 ,求使
,求使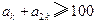 的最小正整数
的最小正整数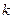 的值.
的值.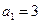 ,
,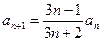
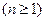 ,求
,求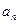 。
。