题目内容
【题目】设![]() ,函数
,函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间
在区间![]() 上有唯一零点,试求a的值.
上有唯一零点,试求a的值.
【答案】(1)![]() 的单调减区间是
的单调减区间是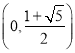 ,单调增区间是
,单调增区间是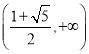 ;(2)
;(2)![]() .
.
【解析】
(1)将![]() 代入
代入![]() 中可得
中可得![]() (
(![]() ),令
),令![]() ,解得
,解得![]() ,进而求得单调区间;
,进而求得单调区间;
(2)令![]() ,解得
,解得![]() (舍),
(舍),![]() ,可得函数
,可得函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,则
上单调递增,则![]() ,由于函数
,由于函数![]() 在区间
在区间![]() 上有唯一零点,则
上有唯一零点,则![]() ,整理即为
,整理即为![]() ,设
,设![]() ,可得
,可得![]() 在
在![]() 是单调递增的,则
是单调递增的,则![]() ,进而求得
,进而求得![]()
(1)函数![]() ,
,
当![]() 时,
时,![]() (
(![]() ),
),
∴![]() ,
,
令![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
∴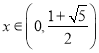 时,
时,![]() ;
;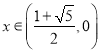 时,
时,![]() ,
,
∴![]() 的单调减区间是
的单调减区间是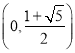 ,单调增区间是
,单调增区间是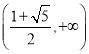
(2)![]() ,
,
则![]() ,
,
令![]() ,得
,得![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴方程的解为![]() (舍),
(舍),![]() ;
;
∴函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,
,
若函数![]() 在区间
在区间![]() 上有唯一零点,
上有唯一零点,
则![]() ,
,
而![]() 满足
满足![]() ,
,
∴![]() ,
,
即![]() ,
,
设![]() ,
,
∵![]() 在
在![]() 是单调递增的,
是单调递增的,
∴![]() 至多只有一个零点,
至多只有一个零点,
而![]() ,
,
∴用![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]()

【题目】某饮水机厂生产的A,B,C,D四类产品,每类产品均有经济型和豪华型两种型号,某一月的产量如下表(单位:台)
A | B | C | D | |
经济型 | 5000 | 2000 | 4500 | 3500 |
豪华型 | 2000 | 3000 | 1500 | 500 |
(1)在这一月生产的饮水机中,用分层抽样的方法抽取n台,其中有A类产品49台,求n的值;
(2)用随机抽样的方法,从C类经济型饮水机中抽取10台进行质量检测,经检测它们的得分如下:7.9,9.4,7.8,9.4,8.6,9.2,10,9.4,7.9,9.4,从D类经济型饮水机中抽取10台进行质量检测,经检测它们的得分如下:8.9,9.3,8.8,9.2,8.6,9.2,9.0,9.0,8.4,8.6,根据分析,你会选择购买C类经济型饮水机与D类经济型饮水机中哪类产品.
【题目】为普及学生安全逃生知识与安全防护能力,某学校高一年级举办了安全知识与安全逃生能力竞赛,该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛,现将所有参赛选手参加笔试的成绩(得分均为整数,满分为![]() 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
分数(分数段) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)求表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)按规定,预赛成绩不低于![]() 分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为
分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
