题目内容
10.若2x+3y+z=7,则x2+y2+z2的最小值为$\frac{7}{2}$.分析 由条件利用柯西不等式(22+32+12)(x2+y2+z2)≥(2x+3y+z)2,求得x2+y2+z2的最小值.
解答 解:12+22+32=14,∴由柯西不等式可得(22+32+12)(x2+y2+z2)≥(2x+3y+z)2=72,
∴x2+y2+z2≥$\frac{49}{14}$=$\frac{7}{2}$,即x2+y2+z2的最小值是$\frac{7}{2}$,
故答案为:$\frac{7}{2}$.
点评 本题主要考查了函数的最值,以及柯西不等式的应用,解题的关键是利用柯西不等式(a2+b2+c2)(x2+y2+z2)≥(ax+by+cz)2,进行解决.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
20.已知f(x)是定义在(0,+∞)上的单调递减函数,f′(x)是其导函数,若 $\frac{f(x)}{f′(x)}$>x,则下列不等关系成立的是( )
| A. | f(2)<2f(1) | B. | 3f(2)>2f(3) | C. | ef(e)<f(e2) | D. | ef(e2)>f(e3) |
 把函数g(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{3}$个单位长度得到函数y=f(x)的图象(如图).
把函数g(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{3}$个单位长度得到函数y=f(x)的图象(如图).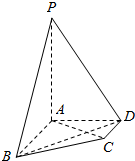 在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=2,AD=$\sqrt{2}$,CD=1,PA⊥平面ABCD,PA=2.
在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=2,AD=$\sqrt{2}$,CD=1,PA⊥平面ABCD,PA=2.