题目内容
5.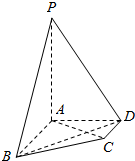 在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=2,AD=$\sqrt{2}$,CD=1,PA⊥平面ABCD,PA=2.
在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=2,AD=$\sqrt{2}$,CD=1,PA⊥平面ABCD,PA=2.(Ⅰ)设平面PAB∩平面PCD=m,求证:CD∥m;
(Ⅱ)设点Q为线段PB上一点,且直线QC与平面PAC所成角的正切值为$\frac{\sqrt{2}}{2}$,求$\frac{PQ}{PB}$的值.
分析 (Ⅰ)由AB∥CD,得到CD∥平面PAB,由此利用平面PAB∩平面PCD=m,能证明CD∥m.
(Ⅱ)设$\frac{PQ}{PB}=λ$,以A为原点,AB为x轴,以AD为y轴,以AP为z轴,建立空间直角坐标系,利用向量法能求出$\frac{PQ}{PB}$的值.
解答 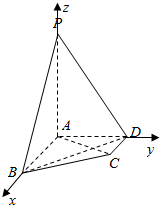 (Ⅰ)证明:∵AB∥CD,CD?平面PAB,AB?平面PAB,
(Ⅰ)证明:∵AB∥CD,CD?平面PAB,AB?平面PAB,
∴CD∥平面PAB,
∵CD?平面PCD,平面PAB∩平面PCD=m,
∴CD∥m.…(4分)
(Ⅱ)解:设$\frac{PQ}{PB}=λ$,∵AB⊥AD,PD⊥平面ABCD,
∴以A为原点,AB为x轴,以AD为y轴,以AP为z轴,建立如图所示的空间直角坐标系,
设 Q(x,y,z),直线QC与平面PAC所成角为θ,$\overrightarrow{PQ}=λ\overrightarrow{PB}$,0≤λ≤1,
由已知得P(0,0,2),B(2,0,0),C(1,$\sqrt{2}$,0),
∴(x,y,z-2)=λ(2,0,-2)=(2λ,0,-2λ),
∴Q(2λ,0,-2λ+2),…(6分)
∴$\overrightarrow{CQ}$=(2λ-1,-$\sqrt{2}$,-2λ+2),…(7分)$\overrightarrow{AP}$=(0,0,2),$\overrightarrow{AC}$=(1,$\sqrt{2}$,0),
平面PAC的一个法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AP}=2c=0}\\{\overrightarrow{n}•\overrightarrow{AC}=a+\sqrt{2}b=0}\end{array}\right.$.取a=$\sqrt{2}$,得$\overrightarrow{n}$=($\sqrt{2},-1,0$),…(9分)
∵直线QC与平面PAC所成角的正切值为$\frac{\sqrt{2}}{2}$,∴tan$θ=\frac{\sqrt{2}}{2}$,
∴cosθ=|$\frac{\overrightarrow{n}•\overrightarrow{CQ}}{|\overrightarrow{n}|•|\overrightarrow{CQ}|}$|=$\frac{\sqrt{3}}{3}$,∴|$\frac{\sqrt{2}(2λ-1)+\sqrt{2}}{\sqrt{3}•\sqrt{(2λ-1)^{2}+2+(-2λ+2)^{2}}}$|=$\frac{\sqrt{3}}{3}$,解得$λ=\frac{7}{12}$.…(11分)
∴$\frac{PQ}{PB}$=$\frac{7}{12}$.…(12分)
点评 本题考查两直线平行的证明,考查两线段比值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
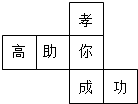 水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )
水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )| A. | 左面,后面,上面 | B. | 后面,上面,左面 | C. | 上面,左面,后面 | D. | 后面,左面,上面 |
| A. | 1 | B. | 2 | C. | 3 | D. | 1或3 |