题目内容
【题目】已知函数f(x)=(x﹣1)|x﹣a|﹣x﹣2a(x∈R).
(1)若a=﹣1,求方程f(x)=1的解集;
(2)若![]() ,试判断函数y=f(x)在R上的零点个数.
,试判断函数y=f(x)在R上的零点个数.
【答案】(1)![]() .(2)答案见解析
.(2)答案见解析
【解析】
(1)因式分解即可求解方程;
(2)对a分类讨论求解零点个数.
(1)当a=﹣1时,由f(x)=1得:(x﹣1)|x+1|﹣(x﹣1)=0,即(x﹣1)(|x+1|﹣1)=0,
解得x=1或|x+1|=1,则有x=1或x=0或x=﹣2,
即解集为{0,1,﹣2};
(2)f(x)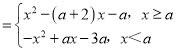 ,
,
当a=0时,f(x)=(x﹣1)|x|﹣x,由f(x)=0,可得x=0,2,两个零点;
当0<a<2时,当x<a时,f(x)=﹣(x![]() )2
)2![]() a(a﹣12),
a(a﹣12),
![]() a<a,可得f(x)在(﹣∞,
a<a,可得f(x)在(﹣∞,![]() a)递增,(
a)递增,(![]() a,a)递减,即f(x)在x<a有最大值
a,a)递减,即f(x)在x<a有最大值![]() a(a﹣12)<0,
a(a﹣12)<0,
当x≥a时,f(x)=(x![]() )2
)2![]() (a+4)2+3,
(a+4)2+3,![]() a,
a,
可得f(x)在(a,![]() a+1)递减,(
a+1)递减,(![]() a+1,+∞)递增,
a+1,+∞)递增,
即f(x)在x≥a有最小值![]() (a+4)2+3<0,
(a+4)2+3<0,
且在x→﹣∞时,f(x)→﹣∞;在x→+∞时,f(x)→+∞,则f(x)在0<a<2时,只有一个零点;
当![]() a<0时,当x<a时,f(x)=﹣(x
a<0时,当x<a时,f(x)=﹣(x![]() )2
)2![]() a(a﹣12),
a(a﹣12),
![]() a>a,可得f(x)在(﹣∞,a)递增,即f(x)在x<a时,f(x)<f(a)=﹣3a>0,
a>a,可得f(x)在(﹣∞,a)递增,即f(x)在x<a时,f(x)<f(a)=﹣3a>0,
当x≥a时,f(x)=(x![]() )2
)2![]() (a+4)2+3,
(a+4)2+3,![]() a,
a,
可得f(x)在(a,![]() a+1)递减,(
a+1)递减,(![]() a+1,+∞)递增,
a+1,+∞)递增,
即f(x)在x≥a有最小值![]() (a+4)2+3<0,
(a+4)2+3<0,
且在x→﹣∞时,f(x)→﹣∞;在x→+∞时,f(x)→+∞,则f(x)在![]() a<0时,有三个零点;
a<0时,有三个零点;
综上可得y=f(x)在R上的零点个数:
当![]() ,一个零点,当
,一个零点,当![]() ,两个零点,当
,两个零点,当![]() ,三个零点
,三个零点

【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
参数数据及公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,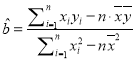 ,
,![]() ,
,![]() .
.
(1)若用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)用对数回归模型拟合y与x的关系,可得回归方程:![]() ,经计算得出线性回归模型和对数模型的
,经计算得出线性回归模型和对数模型的![]() 分别约为0.75和0.97,请用
分别约为0.75和0.97,请用![]() 说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.