题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c,已知acosB+bcosA=csinC,b2+c2-a2=
bc,则B=( )
| 3 |
A.
| B.
| C.
| D.
|
∵b2+c2-a2=
bc,
∴cosA=
=
=
,
解得A=
,
∵acosB+bcosA=csinC,
∴由正弦定理得sinAcosB+sinBcosA=sinCsinC,
即sin(A+B)=sinC=sinCsinC,
∴sinC=1,即C=
,
∴B=
.
故选:B
| 3 |
∴cosA=
| b2+c2-a2 |
| 2bc |
| ||
| 2bc |
| ||
| 2 |
解得A=
| π |
| 6 |
∵acosB+bcosA=csinC,
∴由正弦定理得sinAcosB+sinBcosA=sinCsinC,
即sin(A+B)=sinC=sinCsinC,
∴sinC=1,即C=
| π |
| 2 |
∴B=
| π |
| 3 |
故选:B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
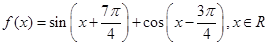 .
.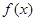 的最小正周期和最值;
的最小正周期和最值;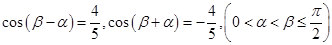 , 求证:
, 求证: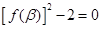 .
.
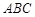 的面积是
的面积是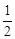 ,
,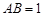 ,
,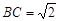 ,则
,则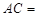 ( )
( )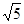
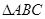 中,由已知条件解三角形,其中有两解的是( )
中,由已知条件解三角形,其中有两解的是( )