已知△ABC中三内角A.B.C的对边分别是a.b.c.若B=30°.b=1.c=3.则△ABC的面积为( )A．32B．34C．32或34D．32或3 题目和参考答案——青夏教育精英家教网——

题目内容

已知△ABC中三内角A，B，C的对边分别是a，b，c，若B=30°，b=1，c=

3

，则△ABC的面积为（　　）

A．

3

2

B．

3

4

C．

3

2

或

3

4

D．

3

2

或

3

∵B=30°，b=1，c=

3

，
∴由余弦定理得：b²=a²+c²-2accosB，即1=a²+3-3a，
解得：a=1或a=2，
当a=1时，S_△ABC=

1

2

acsinB=

3

4

；当a=2时，S_△ABC=

1

2

acsinB=

3

2

．
故选C

练习册系列答案

地理图册系列答案

第一测评系列答案

点金系列答案

点睛学案系列答案

夺冠金卷单元同步测试系列答案

夺冠课时导学案系列答案

发现会考系列答案

发展性评价系列答案

仿真试卷系列答案

非常好冲刺系列答案

相关题目

如图所示，点O为做简谐运动的物体的平衡位置，取向右的方向为物体位移的正方向，若已知振幅为3 cm，周期为3 s，且物体向右运动到A点(距平衡位置最远处)开始计时．(1)求物体离开平衡位置的位移x(cm)和时间t(s)之间的函数关系式；(2)求该物体在t＝5 s时的位置．

下列判断正确的是（　　）

A．a=7，b=14，A=30°，有两解

B．a=30，b=25，A=150°，有一解

C．a=6，b=9，A=45°，有两解

D．a=9，b=10，A=60°，无解

已知a，b，c分别为△ABC三个内角A，B，C的对边，c=

asinC-ccosA
（1）求角A；
（2）若a=2，△ABC的面积为

已知函数f（x）=（

sinωx+cosωx）cosωx-

（ω＞0）最小正周期为4π
（1）求f（x）的单调递增区间
（2）在△ABC中，角A、B、C的对边分别是a、b、c，满足（2a-c）cosB=bcosC，求函数f（2C）的取值范围．

在△ABC中，内角A，B，C的对边分别为a，b，c，已知acosB+bcosA=csinC，b²+c²-a²=

bc，则B=（　　）

根据下列条件解三角形，两解的是（）

A．b = 10，A = 45°，B = 70°

B．a = 60，c = 48，B = 100°

C．a = 14，b = 16，A = 45°

D．a = 7，b = 5，A = 80°

轮船A和轮船B在中午12时同时离开海港C，两船航行方向的夹角为120°，两船的航行速度分别为

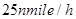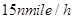，则下午2时两船之间的距离是_______nmile。