题目内容
已知数列{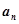 }、{
}、{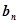 }、{
}、{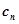 }满足
}满足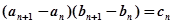 ,
,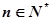 .
.
(1)设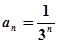 ,
,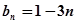 ,求数列{
,求数列{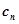 }的前n项和Sn;
}的前n项和Sn;
(2)设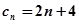 ,{
,{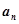 }是公差为2的等差数列,若
}是公差为2的等差数列,若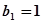 ,求{
,求{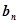 }的通项公式;
}的通项公式;
(3)设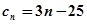 ,
,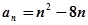 ,求证整数k使得对一切
,求证整数k使得对一切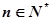 ,均有bn≥bk.
,均有bn≥bk.
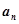 }、{
}、{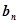 }、{
}、{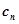 }满足
}满足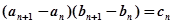 ,
,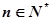 .
.(1)设
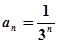 ,
,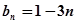 ,求数列{
,求数列{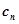 }的前n项和Sn;
}的前n项和Sn; (2)设
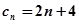 ,{
,{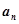 }是公差为2的等差数列,若
}是公差为2的等差数列,若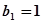 ,求{
,求{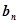 }的通项公式;
}的通项公式;(3)设
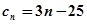 ,
,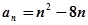 ,求证整数k使得对一切
,求证整数k使得对一切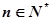 ,均有bn≥bk.
,均有bn≥bk.(1)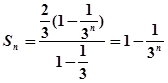 ;(2)
;(2)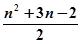 ;(3)见解析.
;(3)见解析.
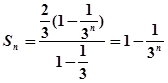 ;(2)
;(2)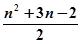 ;(3)见解析.
;(3)见解析.本试题主要考查了数列的求和以及等差数列的通项公式的运用。
解: (1) ……………1分
……………1分
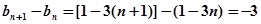 ……………2分
……………2分
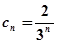
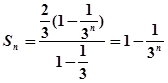 ……………4分
……………4分
(2)易得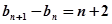 , ……………5分
, ……………5分
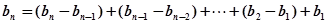 ……………6分
……………6分
=(n+1)+n+(n-1)+…+3+1=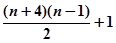 =
=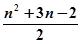 ……………8分
……………8分
(3)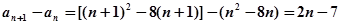
\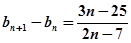 ……………9分
……………9分
由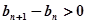 得
得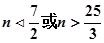
又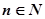 ,
,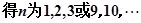
由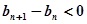 得
得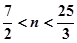
又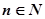 ,
,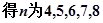 ……………11分
……………11分
\数列{bn}中,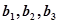 递增,
递增,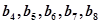 递减,
递减, 递增,
递增,
\最小项为b1或b8. ……………13分
又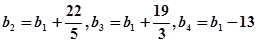
\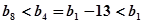
\最小项为b8.故有k=8使得对一切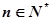 ,均有bn≥bk. ……………14分
,均有bn≥bk. ……………14分
解: (1)
 ……………1分
……………1分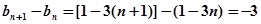 ……………2分
……………2分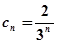
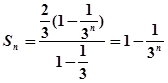 ……………4分
……………4分(2)易得
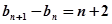 , ……………5分
, ……………5分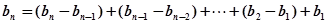 ……………6分
……………6分=(n+1)+n+(n-1)+…+3+1=
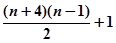 =
=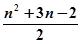 ……………8分
……………8分(3)
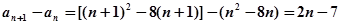
\
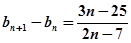 ……………9分
……………9分由
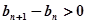 得
得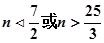
又
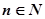 ,
,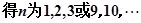
由
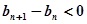 得
得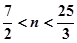
又
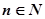 ,
,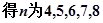 ……………11分
……………11分\数列{bn}中,
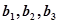 递增,
递增,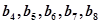 递减,
递减, 递增,
递增,\最小项为b1或b8. ……………13分
又
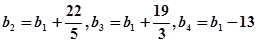
\
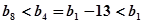
\最小项为b8.故有k=8使得对一切
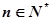 ,均有bn≥bk. ……………14分
,均有bn≥bk. ……………14分
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
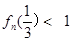 .
.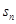 =
=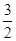
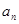 -3,那么这个数列的通项公式是_______.
-3,那么这个数列的通项公式是_______.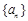 为等比数列,首项
为等比数列,首项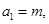 公比
公比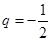 ,数列
,数列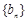 满足
满足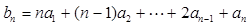 ,
,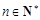 .
.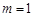 时,求
时,求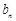 ;
;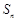 为数列
为数列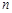 项和,若对于任意的正整数
项和,若对于任意的正整数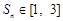 ,求实数
,求实数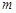 的取值范围.
的取值范围.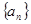 中,
中,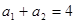 ,
,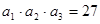 ,则
,则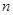 项和
项和 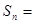 _____
_____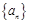 的前
的前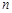 项和为
项和为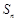 ,若
,若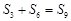 ,则数列
,则数列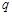 是 .
是 .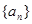 的前n项和为
的前n项和为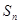 ,且
,且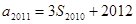 ,
, 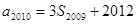 ,则公比
,则公比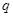 等于 ( )
等于 ( )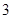
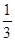
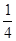
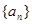 的前
的前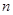 项和为
项和为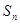 ,对任意
,对任意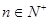 都有
都有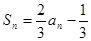 ,若
,若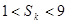
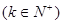 ,则
,则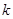 的值为___
的值为___ 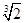 等比数列
等比数列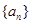 的各项都是正数,且
的各项都是正数,且 ,则( )
,则( )