Question

【题目】如图，抛物线关于x轴对称，它的顶点在坐标原点，点P（1，2），A（x1 ， y1），B（x2 ， y2）均在抛物线上．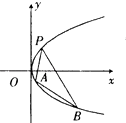

（1）求该抛物线方程；
（2）若AB的中点坐标为（1，﹣1），求直线AB方程．

Answer 1

【答案】
（1）解：由题意可设抛物线方程为y2=2px（p＞0），

∵P（1，2）在抛物线上，

∴22=2p，即p=2．

∴抛物线方程为：y2=4x；

（2）解：∵A（x1，y1），B（x2，y2）在抛物线上，

∴ ， ．

两式作差得：（y1﹣y2）（y1+y2）=4（x1﹣x2），

．

又AB的中点坐标为（1，﹣1），

∴y1+y2=﹣2，

则 ．

∴直线AB方程为y+1=﹣2（x﹣1），

即2x+y﹣1=0．

【解析】（1）由题意设出抛物线方程，代入P点坐标求p，则抛物线方程可求；（2）把A，B的坐标代入抛物线方程，作差后结合AB的中点坐标求出AB所在直线的斜率，由点斜式得AB所在直线方程．