题目内容
【题目】已知A、B分别为椭圆E:![]() (a>1)的左、右顶点,G为E的上顶点,
(a>1)的左、右顶点,G为E的上顶点,![]() ,P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
,P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
(1)求E的方程;
(2)证明:直线CD过定点.
【答案】(1)![]() ;(2)证明详见解析.
;(2)证明详见解析.
【解析】
(1)由已知可得:![]() ,
, ![]() ,
,![]() ,即可求得
,即可求得![]() ,结合已知即可求得:
,结合已知即可求得:![]() ,问题得解.
,问题得解.
(2)设![]() ,可得直线
,可得直线![]() 的方程为:
的方程为:![]() ,联立直线
,联立直线![]() 的方程与椭圆方程即可求得点
的方程与椭圆方程即可求得点![]() 的坐标为
的坐标为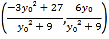 ,同理可得点
,同理可得点![]() 的坐标为
的坐标为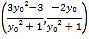 ,当
,当![]() 时,可表示出直线
时,可表示出直线![]() 的方程,整理直线
的方程,整理直线![]() 的方程可得:
的方程可得: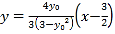 即可知直线过定点
即可知直线过定点![]() ,当
,当![]() 时,直线
时,直线![]() :
:![]() ,直线过点
,直线过点![]() ,命题得证.
,命题得证.
(1)依据题意作出如下图象:
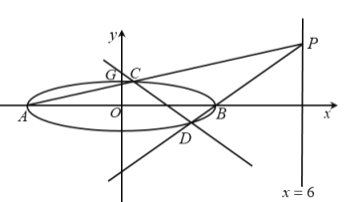
由椭圆方程![]() 可得:
可得:![]() ,
, ![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() 椭圆方程为:
椭圆方程为:![]()
(2)证明:设![]() ,
,
则直线![]() 的方程为:
的方程为:![]() ,即:
,即:![]()
联立直线![]() 的方程与椭圆方程可得:
的方程与椭圆方程可得: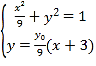 ,整理得:
,整理得:
![]() ,解得:
,解得:![]() 或
或![]()
将![]() 代入直线
代入直线![]() 可得:
可得:![]()
所以点![]() 的坐标为
的坐标为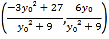 .
.
同理可得:点![]() 的坐标为
的坐标为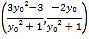
当![]() 时,
时,
![]() 直线
直线![]() 的方程为:
的方程为: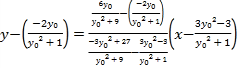 ,
,
整理可得: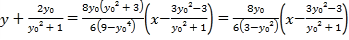
整理得: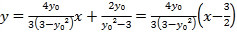
所以直线![]() 过定点
过定点![]() .
.
当![]() 时,直线
时,直线![]() :
:![]() ,直线过点
,直线过点![]() .
.
故直线CD过定点![]() .
.

练习册系列答案
相关题目