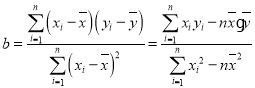题目内容
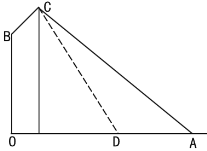
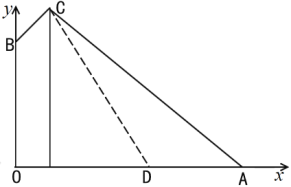
【题目】如图，在路边安装路灯：路宽
米，灯杆长
米，且与灯柱
成120°角，路灯采用锥形灯罩，灯罩轴线
与灯杆垂直且正好通过道路路面的中线.
（1）求灯柱高的长度（精确到0.01米）；
（2）若该路灯投射出的光成一个圆锥体，该圆锥体母线与轴线的夹角是30°，写出路灯在路面上投射出的截面图形的边界是什么曲线？写出其相应的几何量（精确到0.01米）.
【答案】（1）16.25米；（2）边界是椭圆，长轴长为31.61米，短轴长为21.07米，焦距长为23.56米.
【解析】
（1）先建立平面直角坐标系，再求出直线的点斜式方程即可；
（2）路灯在路面上投射出的截面图形的边界是椭圆，再求出其长轴长、短轴长及焦距长即可.
解：（1）建立以
为坐标原点，
所在直线为
轴，
所在直线为
轴的直角坐标系，设
，则
，因为直线
的倾斜角为120°，
所以直线的方程为：
，
将
代入得：
，所以 
米；
（2）路灯在路面上投射出的截面图形的边界是椭圆，
由已知可得该椭圆的长轴长为
米，
短轴长为
米，
焦距长为
米.
字词句篇与同步作文达标系列答案【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，12月1日至12月5日的昼夜温差与实验室每天每100颗种子中的发芽数如下表所示：
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差x(℃) | 10 | 11 | 13 | 12 | 8 |
发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是：先从这5组数据中选取2组，用剩下的3组数据求回归方程，再用被选取的2组数据进行检验．
(1)求选取的2组数据恰好是不相邻的2组数据的概率．
(2)若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求y关于x的线性回归方程
.
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗，则认为得到的线性回归方程是可靠的，试问(2)中所得的线性回归方程是否可靠？
