题目内容
（1）已知点B（6，0）和C（-6，0），过点B的直线l与过点C的直线m相交于点A，设直线l的斜率为k1，直线m的斜率为k2，如果k1•k2=-
，求点A的轨迹．
（2）用正弦定理证明三角形外角平分线定理：如果在△ABC中，∠A的外角平分线AD与边BC的延长线相交于点D，则
=
．
| 4 |
| 9 |
（2）用正弦定理证明三角形外角平分线定理：如果在△ABC中，∠A的外角平分线AD与边BC的延长线相交于点D，则
| BD |
| DC |
| AB |
| AC |
分析：（1）设出点A坐标为（x，y），用直线的斜率公式将k1、k2表示为关于x、y的式子，结合题意建立关系式，化简可得点A的轨迹是以B、C为焦点的椭圆（除长轴端点除外）．
（2）分别在△ACD、△ABD中根据正弦定理列式，再将所得的式子相除并利用比例的性质，可得
=
成立．
（2）分别在△ACD、△ABD中根据正弦定理列式，再将所得的式子相除并利用比例的性质，可得
| BD |
| DC |
| AB |
| AC |
解答：解：（1）设A点坐标为（x，y），可得直线的斜率为k1=
，
直线m的斜率为k2=
，
结合题意可得
•
=-
，整理得
+
=1 (x≠±6)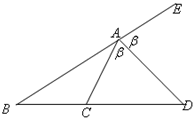
所以点A的轨迹是以B、C为焦点的椭圆（除长轴端点除外）．
（2）设∠CAD=∠DAE=β，
在△ACD中，由正弦定理得
=
…①，
在△ABD中，由正弦定理得
=
，即
=
…②①②两式相除，可得
=
，结论成立．
| y |
| x-6 |
直线m的斜率为k2=
| y |
| x+6 |
结合题意可得
| y |
| x-6 |
| y |
| x+6 |
| 4 |
| 9 |
| x2 |
| 36 |
| y2 |
| 16 |
所以点A的轨迹是以B、C为焦点的椭圆（除长轴端点除外）．
（2）设∠CAD=∠DAE=β，
在△ACD中，由正弦定理得
| DC |
| sinβ |
| AC |
| sin∠D |
在△ABD中，由正弦定理得
| BD |
| sin∠BAD |
| AB |
| sin∠D |
| BD |
| sin∠β |
| AB |
| sin∠D |
| BD |
| DC |
| AB |
| AC |
点评：本题着重考查了动点轨迹方程的求法、直线的斜率公式与椭圆的标准方程，考查了利用正弦定理解三角形等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
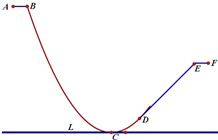如图是A-B-C-D-E-F是一个滑滑板的轨道截面图，其中AB，DE，EF是线段，B-C-D是一抛物线弧；点C是抛物线的顶点，直线DE与抛物线在D处相切，直线L是地平线．已知点B离地面L的高度是9米，离抛物线的对称轴距离是6米，直线DE与L的夹角是45．试建立直角坐标系：