题目内容
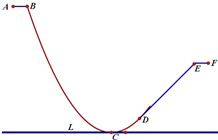 如图是A-B-C-D-E-F是一个滑滑板的轨道截面图,其中AB,DE,EF是线段,B-C-D是一抛物线弧;点C是抛物线的顶点,直线DE与抛物线在D处相切,直线L是地平线.已知点B离地面L的高度是9米,离抛物线的对称轴距离是6米,直线DE与L的夹角是45.试建立直角坐标系:
如图是A-B-C-D-E-F是一个滑滑板的轨道截面图,其中AB,DE,EF是线段,B-C-D是一抛物线弧;点C是抛物线的顶点,直线DE与抛物线在D处相切,直线L是地平线.已知点B离地面L的高度是9米,离抛物线的对称轴距离是6米,直线DE与L的夹角是45.试建立直角坐标系:(Ⅰ)求抛物线方程,并确定D点的位置;
(Ⅱ)现将抛物线弧B-C-D改造成圆弧,要求圆弧经过点B,D,且与直线DE在D处相切.试判断圆弧与地平线L的位置关系,并求该圆弧长.(可参考数据
| 3 |
| 2 |
分析:(Ⅰ) 以C为原点,L所在的直线为X轴,如图所示建立直角坐标系,则B(-6,9). 设抛物线的方程为y=ax2,把点B(-6,9)代入y=ax2,求出a即可
(Ⅱ)由圆的切线性质及垂径定理,设所求圆的圆心为H.则H在过D与DE垂直的直线l1 上,又在BD的中垂线上,解出圆心,半径,再利用直线与圆的位置关系去解.
(Ⅱ)由圆的切线性质及垂径定理,设所求圆的圆心为H.则H在过D与DE垂直的直线l1 上,又在BD的中垂线上,解出圆心,半径,再利用直线与圆的位置关系去解.
解答: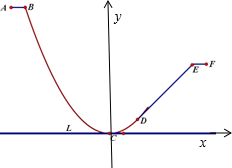 解:(Ⅰ)以C为原点,L所在的直线为X轴,如图所示建立直角坐标系,则B(-6,9).
解:(Ⅰ)以C为原点,L所在的直线为X轴,如图所示建立直角坐标系,则B(-6,9).
设抛物线的方程为y=ax2,把点B(-6,9)代入y=ax2得a=
,
故抛物线方程为y=
x2.
设D(x0,
x02),根据直线DE与L的夹角是45.得直线L的斜率为1,由y′=
x,
∴
x0=1,∴x0=2,
故D点的坐标是(2,1).
(Ⅱ)设所求圆的圆心为H.过D与L垂直的直线方程是l1:y=-x+3,BD的中点坐标是(-2,5),kBD=-1,故BD中垂线方程是y=x+7,
由
得x=-2,y=5.∴H(-2,5).∵B(-6,9)∈l1,∴BD是直径.
∵BD=8
,半径r=4
.∴
=4
π≈17.7(m).
∵圆心H到L的距离为d=5,d=5<4
=r,故圆弧与地平线L相交.
 解:(Ⅰ)以C为原点,L所在的直线为X轴,如图所示建立直角坐标系,则B(-6,9).
解:(Ⅰ)以C为原点,L所在的直线为X轴,如图所示建立直角坐标系,则B(-6,9). 设抛物线的方程为y=ax2,把点B(-6,9)代入y=ax2得a=
| 1 |
| 4 |
故抛物线方程为y=
| 1 |
| 4 |
设D(x0,
| 1 |
| 4 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
故D点的坐标是(2,1).
(Ⅱ)设所求圆的圆心为H.过D与L垂直的直线方程是l1:y=-x+3,BD的中点坐标是(-2,5),kBD=-1,故BD中垂线方程是y=x+7,
由
|
∵BD=8
| 2 |
| 2 |
 |
| BD |
| 2 |
∵圆心H到L的距离为d=5,d=5<4
| 2 |
点评:本题考查圆锥曲线方程求解,直线与圆的位置关系、函数与导数知识,考查建模能力、分析解决问题、计算能力.是好题.

练习册系列答案
相关题目
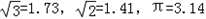 ,精确到0.1米)
,精确到0.1米)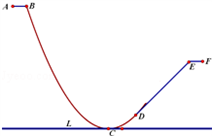
 (可参考数据
(可参考数据 ,精确到0.1米)
,精确到0.1米)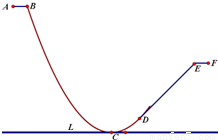
 ,精确到0.1米)
,精确到0.1米)