Question

（1）已知点A（5，0），点B在直线y=6上运动，点C单位圆x²+y²=1运动，求AB+BC的最小值及对应点B的坐标．
（2）点P在直线y=6上运动，过点P作单位圆x²+y²=1的两切线，设两切点为Q和R，求证：直线QR恒过定点，并求出定点坐标．

Answer 1

分析：（1）如图所示，作出点A（5，0）关于直线y=6的对称点A′（5，12），则AB=A′B．可得AB+BC=A′B+BC，连接OA交直线y=6于点B，交⊙O于点C．则AB+BC的最小值=OA-r．
（2）利用圆的切线的性质可得：两个切点Q，R在以OP为的圆上，与x²+y²=1即可得到过两个圆的交点Q，R的直线方程，再利用直线系的性质即可得出直线所过的定点．

解答：解：（1）如图所示，作出点A（5，0）关于直线y=6的对称点A′（5，12），则AB=A′B．
∴AB+BC=A′B+B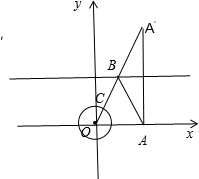C，
连接OA交直线y=6于点B，交⊙O于点C．
则AB+BC的最小值=OA-r=

52+122

-1=12．
此时直线OA：y=

12

5

x，
令y=6，解得x=

5

2

．
∴B(

5

2

，6)，．
∴AB+BC的最小值为12，对应点B的坐标为(

5

2

，6)
（2）设P（s，6），则OP的中点为M(

s

2

，3)．
∴以点M为圆心，OM为半径的圆的方程为：(x-

s

2

)2+(y-3)2=

s2

4

+9，
化为x²-sx+y²-6y=0，
联立

x2+y2=1 x2-sx+y2-6y=0

，
化为sx+6y-1=0即为过两个圆的交点Q，R的直线方程．．
联立

x=0 y- 1 6 =0

，
解得

x=0 y= 1 6

．
∴直线QR恒过定点(0，

1

6

)．

点评：本题综合考查了圆的标准方程及其性质、切线的性质、圆的根轴的求法，属于难题．