题目内容
已知点B(6,0)和点C(-6,0),过点B的直线l与过点C的直线m相交于点A,设直线l的斜率为k1,直线m的斜率为k2,
(1)如果k1•k2=-
,求点A的轨迹方程,并写出此轨迹曲线的焦点坐标;
(2)如果k1•k2=
,求点A的轨迹方程,并写出此轨迹曲线的离心率;
(3)如果k1•k2=k(k≠0,k≠-1),根据(1)和(2),你能得到什么结论?(不需要证明所得结论)
(1)如果k1•k2=-
| 4 |
| 9 |
(2)如果k1•k2=
| 4 |
| 9 |
(3)如果k1•k2=k(k≠0,k≠-1),根据(1)和(2),你能得到什么结论?(不需要证明所得结论)
分析:(1)求出直线l、m的斜率,利用k1•k2=-
,化简方程,即可求得结论;
(2)求出直线l、m的斜率,利用k1•k2=
,化简方程,即可求得结论;
(3)求出直线l、m的斜率,利用k1•k2=k,化简方程,对参数讨论,即可求得结论;
| 4 |
| 9 |
(2)求出直线l、m的斜率,利用k1•k2=
| 4 |
| 9 |
(3)求出直线l、m的斜率,利用k1•k2=k,化简方程,对参数讨论,即可求得结论;
解答:解:(1)直线l过点B(6,0),斜率为k1,则其直线方程为:y-0=k1(x-6),所以,k1=
同理,k2=
∵k1•k2=-
,∴
•
=-
,
∴9y2=-4(x2-36)
∴
+
=1,它表示椭圆,焦点坐标为(±2
,0);
(2)∵k1•k2=
,∴
•
=
,∴9y2=4(x2-36)
∴
-
=1,它表示双曲线,离心率为
;
(3)∵k1•k2=k,∴
•
=k,∴y2=k(x2-36)
∴
-
=1
当k>0时,表示双曲线; 当k<0且k≠-1时,表示椭圆;当k=-1时,表示圆.
| y |
| x-6 |
同理,k2=
| y |
| x+6 |
∵k1•k2=-
| 4 |
| 9 |
| y |
| x-6 |
| y |
| x+6 |
| 4 |
| 9 |
∴9y2=-4(x2-36)
∴
| x2 |
| 36 |
| y2 |
| 16 |
| 5 |
(2)∵k1•k2=
| 4 |
| 9 |
| y |
| x-6 |
| y |
| x+6 |
| 4 |
| 9 |
∴
| x2 |
| 36 |
| y2 |
| 16 |
| ||
| 3 |
(3)∵k1•k2=k,∴
| y |
| x-6 |
| y |
| x+6 |
∴
| x2 |
| 36 |
| y2 |
| 36k |
当k>0时,表示双曲线; 当k<0且k≠-1时,表示椭圆;当k=-1时,表示圆.
点评:本题考查轨迹方程,考查学生的计算能力,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
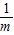 ,那么点A的轨迹一定不是下列曲线(或其一部分)( )
,那么点A的轨迹一定不是下列曲线(或其一部分)( )