题目内容
10.f(x)=2x+sinx为定义在(-1,1)上的函数,则不等式f(1-a)+f(1-2a)<0的解集是($\frac{2}{3}$,1).分析 根据函数奇偶性的定义,证出f(x)是定义在(-1,1)上的奇函数.再由导数恒大于0,得到f(x)是定义在(-1,1)上的增函数.由此将不等式f(1-a)+f(1-2a)<0等价转化为$\left\{\begin{array}{l}{-1<1-a<1}\\{-1<2a-1<1}\\{1-a<2a-1}\end{array}\right.$,解之即可得到原不等式的解集.
解答 解:∵函数解析式为f(x)=2x+sinx,
∴f(-x)=-2x+sin(-x)=-(2x+sinx)=-f(x),
因此函数是定义在(-1,1)上的奇函数.
又∵函数f(x)导数f′(x)=2+cosx>0恒成立,
∴函数f(x)是定义在(-1,1)上的增函数.
因此不等式f(1-a)+f(1-2a)<0,
即f (1-a)<-f (1-2a)=f(2a-1)
可得$\left\{\begin{array}{l}{-1<1-a<1}\\{-1<2a-1<1}\\{1-a<2a-1}\end{array}\right.$,即为$\left\{\begin{array}{l}{0<a<2}\\{0<a<1}\\{a>\frac{2}{3}}\end{array}\right.$,
即有$\frac{2}{3}$<a<1.
∴原不等式的解集为($\frac{2}{3}$,1).
故答案为:($\frac{2}{3}$,1).
点评 本题给出函数f(x)=2x+sinx,要求我们利用单调性和奇偶性解关于x的不等式f (1-a)+f (1-2a)<0,着重考查了函数的基本性质、利用导数研究函数的单调性和一无二次不等式的解法等知识,属于中档题.

练习册系列答案
相关题目
5.设f(x)=2x+3,g(x)=f(x-2),则g(x)等于( )
| A. | 2x+1 | B. | 2x-1 | C. | 2x-3 | D. | 2x+7 |
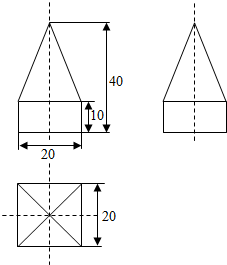 如图所示为一个多面组合体的三视图(单位:cm)
如图所示为一个多面组合体的三视图(单位:cm)