题目内容

13．记$\underset{\stackrel{k}{Ⅱ}}{n=1}$an为数列{an}的前k项积，已知正项等比数列{an}中，若a3，a7是方程x2-6x+2=0的两根，则$\underset{\stackrel{9}{Ⅱ}}{n=1}$an=（　　）
A．8$\sqrt{2}$B．16$\sqrt{2}$C．16D．32

分析 根据根与系数之间的关系，求出a3a7=2，利用等比数列的性质进行求解即可．

解答 解：∵正项等比数列{an}中，若a3，a7是方程x2-6x+2=0的两根，
∴a3a7=2，
则$\underset{\stackrel{9}{Ⅱ}}{n=1}$an=（a3a7）5=25=32，
故选：D

点评 本题主要考查等比数列性质的应用，利用根与系数之间的关系结合等比数列的性质是解决本题的关键．

练习册系列答案
相关题目
3．下列函数中，在区间（0，+∞）上为增函数的是（　　）
A．y=log2（x+5）B．$y={（{\frac{1}{3}}）^x}$C．y=-$\sqrt{x+2}$D．y=$\frac{1}{x}$-x
4．已知点A（-2，1），B（2，5），则线段AB的垂直平分线方程是x+y-3=0．
1．已知p：x2-2（a-1）x+a（a一2）≥0，q：2x2-3x一2≥0，若p是q的必要不充分条件．求实数a的取值范围．
8．已知两直线l1：xcosθ-y（2cos2θ-1）+6=0和l2：2xsinθ+$\sqrt{3}$y+3=0，当l1⊥l2时，θ=$\frac{1}{2}$kπ+$\frac{π}{6}$，k∈Z．
18．若x∈（0，$\frac{π}{2}$），sinxcosx=$\frac{1}{2}$，则$\frac{1}{1+sinx}$+$\frac{1}{1+cosx}$=4-2$\sqrt{2}$．
6．定义在（-1，0）∪（0，+∞）上的函数f（x）及二次函数g（x）满足：f（x）-2f（$\frac{1}{x}$）=ln$\frac{1+x}{{x}^{2}}$，g（1）=g（-3）=3，且g（x）的最小值是-1．
（Ⅰ）求f（x）和g（x）的解析式；
（Ⅱ）若对于x1，x2∈[1，2]，均有g（x1）+ax1≤$\frac{1}{2}$x22+2f（x2）+2ln2-$\frac{1}{2}$成立，求实数a的取值范围；
（Ⅲ）设φ（x）=$\left\{\begin{array}{l}{f（x），（x＞0）}\\{g（x），（x≤0）}\end{array}\right.$，讨论方程φ[φ（x）]=-1的解的个数情况．
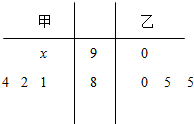3．如图用茎叶图记录了同班的甲、乙两名学生4次数学考试成绩，其中甲的一次成绩模糊不清，用x标记．
（1）若甲、乙这4次的平均成绩相同，确定甲、乙中谁的成绩更稳定，并说明理由；
（2）若甲这4次获得的最高分正好是班上第一名（满分100，且分数为整数），且班上这次数学的第二名是91分，求甲这4次成绩的平均分高于乙这4次成绩的平均分的概率．
4．圆C满足：①圆心C在射线y=2x（x＞0）上；    
②与x轴相切；  
③被直线y=x+2截得的线段长为$\sqrt{14}$
（1）求圆C的方程；
（2）过直线x+y+3=0上一点P作圆C的切线，设切点为E、F，求四边形PECF面积的最小值，并求此时$\overrightarrow{PE}•\overrightarrow{PF}$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网